Question

AB and CD are two identical rods each of length $ l $ and mass $ m $ joined to form a cross is fixed inside a ring of mass $ m $ and radius $ l/2 $ . Moment of inertia of the system about a bisector of the angle between the rods $ \left( {xy} \right) $ is

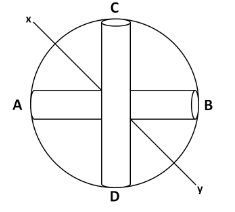
(A) $ \dfrac{{7m{l^2}}}{6} $
(B) $ \dfrac{{13m{l^2}}}{{12}} $
(C) $ \dfrac{{m{l^2}}}{{12}} $
(D) $ \dfrac{{5m{l^2}}}{{24}} $

Answer 1

Hint: To solve this question, we need to find out the moment of inertia of the system about the axis passing through the centre and perpendicular to the plane. We have to use the perpendicular axis theorem for this purpose. Then again using the perpendicular axis theorem and symmetry, we can find out the final value of the moment of inertia about the given axis.

Formula used: The formulae used to solve this question are given by
 $ I = \dfrac{{m{l^2}}}{{12}} $ , here $ I $ is the moment of inertia of a rod of mass $ m $ and length $ l $ about an axis passing through its centre and perpendicular to its length.
 $ I = M{R^2} $ , here $ I $ is the moment of inertia of a ring of mass $ M $ and radius $ R $ about the axis passing through its centre and perpendicular to its plane.

Complete step-by-step solution
Let the moment of inertia be $ {I_{xy}} $ . Let us define two axes in the given system, namely AB and CD by joining the point A, B and C, D respectively as shown in the below diagram. Also, let us name the point of intersection of these axes as O.

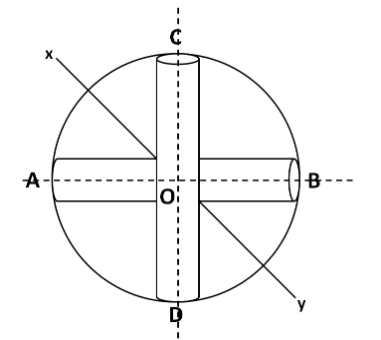
We know that the moment of inertia of a rod about an axis passing through its centre and perpendicular to its length is given by
 $ I = \dfrac{{m{l^2}}}{{12}} $
So the moment of inertia of the rod CD about the AB axis is given by
 $ {I_{AB}} = \dfrac{{m{l^2}}}{{12}} $ ............................(1)
Similarly, the moment of inertia of the rod AB about the CD axis is given by
 $ {I_{CD}} = \dfrac{{m{l^2}}}{{12}} $ ............................(2)
Now, let us consider an axis passing through the point O and perpendicular to the plane of the given system, the o-axis. By perpendicular axis theorem, the moment of inertia of the system of the two rods AB and CD about this axis is given by
 $ {I_{O'}} = {I_{AB}} + {I_{CD}} $
Putting (1) and (2) in the above equation we get
 $ {I_{O'}} = \dfrac{{m{l^2}}}{{12}} + \dfrac{{m{l^2}}}{{12}} $
 $ \Rightarrow {I_{O'}} = \dfrac{{m{l^2}}}{6} $ ............................(3)
Now, we know that the moment of inertia of a ring about the axis passing through its centre and perpendicular to its plane is given by
 $ I = M{R^2} $
According to the question, the mass of the ring is equal to $ m $ and its radius is equal to $ l/2 $ . Therefore substituting $ M = m $ and $ R = \dfrac{l}{2} $ in the above equation, we get the moment of inertia of the given ring about the o-axis as
 $ {I_{O''}} = \dfrac{{m{l^2}}}{4} $ ............................(4)
Adding (4) and (5) we get the total moment of inertia of the system about the o-axis as
 $ {I_O} = \dfrac{{m{l^2}}}{6} + \dfrac{{m{l^2}}}{4} $
 $ \Rightarrow {I_O} = \dfrac{{5m{l^2}}}{{12}} $ ............................(5)
Now, let us consider an axis x’y’ perpendicular to the xy axis, as shown in the below figure.

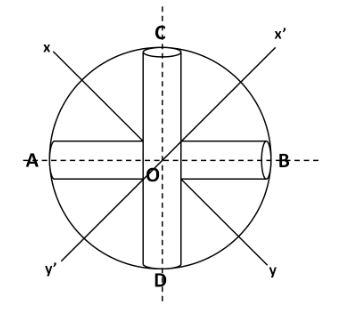
Let the moment of inertia of the system about the x’y’ axis be $ {I_{x'y'}} $ . By symmetry, we can say that
 $ {I_{x'y'}} = {I_{xy}} $
By perpendicular axis theorem, we have
 $ {I_O} = {I_{xy}} + {I_{x'y'}} $
 $ \Rightarrow {I_O} = 2{I_{xy}} $
Putting (5) in the above equation, we get
 $ \dfrac{{5m{l^2}}}{{12}} = 2{I_{xy}} $
 $ \Rightarrow {I_{xy}} = \dfrac{{5m{l^2}}}{{24}} $
Thus, the moment of inertia of the system about the angle bisector is equal to $ \dfrac{{5m{l^2}}}{{24}} $ .
Hence, the correct answer is option D.

Note
Do not forget to include the moment of inertia of the ring while calculating the moment of inertia of the system. The ring has a finite mass. So it will contribute to the moment of inertia of the system.