Question

AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD. Show that $\angle A>\angle C$ and $\angle B>\angle C$

Answer 1

Hint: To solve this question, firstly we will do construction by joining vertex A and C, and B and D. then we will star proving first for $\angle A>\angle C$ and then for $\angle B>\angle C$, by using simple property of triangle which is angle opposite to shortest side is smallest angle and angle opposite to longest side is largest angle in triangle.

Complete step-by-step answer:
Let us first draw the diagram of quadrilateral ABCD according to data given in question.

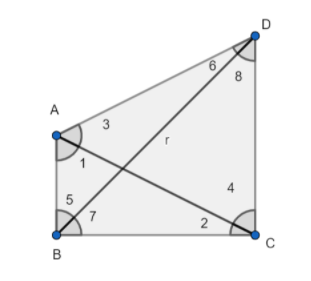
Now, in question it is given that side AB is the smallest side of quadrilateral and CD is largest side of quadrilateral ABCD.
Let us join the vertex A to C with line AC and B to D with line BD.
Also, let \[\angle BAC=\angle 1\], \[\angle BCA=\angle 2\],\[\angle DAC=\angle 3\], \[\angle DCA=\angle 4\], \[\angle ABD=\angle 5\], \[\angle CBD=\angle 7\], \[\angle ADB=\angle 6\] and \[\angle BDC=\angle 8\].
Now, we know the property of a triangle, that angle opposite to shortest side is smallest angle and angle opposite to longest side is largest angle in triangle.
So, in $\vartriangle ABC$ , we can see that
BC > AB, which means angle opposite to side BC will be the largest angle and side opposite to side AB will be the smallest angle.
Hence, \[\angle 1>\angle 2\]……( i )
Now, in triangle $\vartriangle ACD$ , we can see that
CD > AD, which means angle opposite to side CD will be the largest angle and side opposite to side AD will be the smallest angle.
Hence, \[\angle 3>\angle 4\]……( ii )
Now, adding equation ( i ) and equation ( ii ), we get
\[\angle 1+\angle 3>\angle 2+\angle 4\]
From figure we can see that \[\angle DAB=\angle 3+\angle 1\] and \[\angle BCD=\angle 2+\angle 4\] which means
$\angle A>\angle C$
Now, in $\vartriangle BCD$ , we can see that
CD < BD, which means angle opposite to side CD will be largest angle and side opposite to side BD will be smallest angle.
Hence, \[\angle 7>\angle 4\]……( iii )
Now, in triangle $\vartriangle ABD$ , we can see that
AB < AD, which means angle opposite to side AD will be largest angle and side opposite to side AB will be smallest angle.
Hence, \[\angle 5>\angle 2\]……( iv )
Now, adding equation ( i ) and equation ( ii ), we get
\[\angle 7+\angle 5>\angle 6+\angle 8\]
From figure we can see that \[\angle ABC=\angle 5+\angle 7\] and \[\angle ADC=\angle 2+\angle 4\] which means
$\angle B>\angle C$
Hence, if AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD then $\angle B>\angle C$ and $\angle A>\angle C$.

Note: Always make a figure before proving such questions where you need to do constructions. Always remember the property of triangle, that angle opposite to shortest side is smallest angle and angle opposite to longest side is largest angle in triangle. Always mention angle with symbol $\angle $.