Question

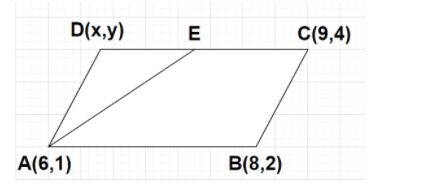
A(6,1), B(8,2) and C(9,4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of $\vartriangle $ADE.
${\text{A}}{\text{. 6}}$ sq. units
${\text{B}}{\text{. }}\dfrac{3}{2}$ sq. units
${\text{C}}{\text{. }}\dfrac{3}{4}$ sq. units
${\text{D}}{\text{. 12}}$ sq. units

Answer 1

Hint: Here, we will proceed by finding out the coordinates of the vertex D of the parallelogram ABCD using distance formula i.e., $D = \sqrt {{{\left( {d - b} \right)}^2} + {{\left( {c - a} \right)}^2}} $ and property of the parallelogram i.e., the pair of any two opposite sides are always equal in length.

Complete step-by-step answer:
Let us consider a parallelogram ABCD having vertices as A(6,1), B(8,2), C(9,4) and D(x,y). Point E is the midpoint of side DC as shown in the figure.
As we know that according to distance formula, the distance between any two points (a,b) and (c,d) is given by
$D = \sqrt {{{\left( {d - b} \right)}^2} + {{\left( {c - a} \right)}^2}} {\text{ }} \to {\text{(1)}}$
Using equation (1), the distance between the points A(6,1) and B(8,2) is given by
AB = $\sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {8 - 6} \right)}^2}} = \sqrt {{1^2} + {2^2}} = \sqrt {1 + 4} = \sqrt 5 $ units
Using equation (1), the distance between the points B(8,2) and C(9,4) is given by
BC = $\sqrt {{{\left( {4 - 2} \right)}^2} + {{\left( {9 - 8} \right)}^2}} = \sqrt {{2^2} + {1^2}} = \sqrt {4 + 1} = \sqrt 5 $ units
Using equation (1), the distance between the points C(9,4) and D(x,y) is given by
CD = $\sqrt {{{\left( {y - 4} \right)}^2} + {{\left( {x - 9} \right)}^2}} = \sqrt {\left( {{y^2} + {4^2} - 8y} \right) + \left( {{x^2} + {9^2} - 18x} \right)} $
$ \Rightarrow $CD$ = \sqrt {{y^2} + 16 - 8y + {x^2} + 81 - 18x} = \sqrt {{y^2} - 8y + {x^2} - 18x + 97} $units
Using equation (1), the distance between the points D(x,y) and A(6,1) is given by
$ \Rightarrow $DA = $\sqrt {{{\left( {1 - y} \right)}^2} + {{\left( {6 - x} \right)}^2}} = \sqrt {\left( {{1^2} + {y^2} - 2y} \right) + \left( {{6^2} + {x^2} - 12x} \right)} $
$ \Rightarrow $DA = $\sqrt {1 + {y^2} - 2y + 36 + {x^2} - 12x} = \sqrt {{y^2} - 2y + {x^2} - 12x + 37} $ units
According to the property of parallelogram, the pair of any two opposite sides are always equal in length
i.e., For any parallelogram ABCD, AB = CD and BC = DA
By substituting the values of AB, BC, CD and DA obtained in the above two equations, we get
$ \Rightarrow \sqrt 5 = \sqrt {{y^2} - 8y + {x^2} - 18x + 97} $ and $ \Rightarrow \sqrt 5 = \sqrt {{y^2} - 2y + {x^2} - 12x + 37} $
Squaring on both sides of the above two equations, we get
$\begin{gathered}
   \Rightarrow 5 = {y^2} - 8y + {x^2} - 18x + 97 \\
   \Rightarrow {y^2} - 8y + {x^2} - 18x + 92 = 0{\text{ }} \to {\text{(2)}} \\
\end{gathered} $ and
 $\begin{gathered}
   \Rightarrow 5 = {y^2} - 2y + {x^2} - 12x + 37 \\
   \Rightarrow {y^2} - 2y + {x^2} - 12x + 32 = 0{\text{ }} \to {\text{(3)}} \\
 \end{gathered}$
By subtracting equation (2) from equation (3), we get
\[
   \Rightarrow {y^2} - 2y + {x^2} - 12x + 32 - \left( {{y^2} - 8y + {x^2} - 18x + 92} \right) = 0 - 0 \\
   \Rightarrow {y^2} - 2y + {x^2} - 12x + 32 - {y^2} + 8y - {x^2} + 18x - 92 = 0 \\
   \Rightarrow 6x + 6y - 60 = 0 \\
   \Rightarrow 6\left( {x + y} \right) = 60 \\
   \Rightarrow x + y = \dfrac{{60}}{6} \\
   \Rightarrow x + y = 10 \\
   \Rightarrow x = 10 - y{\text{ }} \to {\text{(4)}} \\
 \]
By substituting the value of x from equation (4) in equation (2), we get
\[
   \Rightarrow {y^2} - 8y + {\left( {10 - y{\text{ }}} \right)^2} - 18\left( {10 - y{\text{ }}} \right) + 92 = 0 \\
   \Rightarrow {y^2} - 8y + \left( {100 + {y^2} - 20y} \right) - \left( {180 - 18y{\text{ }}} \right) + 92 = 0 \\
   \Rightarrow {y^2} - 8y + 100 + {y^2} - 20y - 180 + 18y + 92 = 0 \\
   \Rightarrow 2{y^2} - 10y + 12 = 0 \\
   \Rightarrow 2\left( {{y^2} - 5y + 6} \right) = 0 \\
   \Rightarrow {y^2} - 5y + 6 = 0 \\
 \]
The above quadratic equation in y can be solved by splitting the middle term method.
\[
   \Rightarrow {y^2} - 2y - 3y + 6 = 0 \\
   \Rightarrow y\left( {y - 2} \right) - 3\left( {y - 2} \right) = 0 \\
   \Rightarrow \left( {y - 3} \right)\left( {y - 2} \right) = 0 \\
 \]
Either \[
  y - 3 = 0 \\
   \Rightarrow y = 3 \\
 \] or \[
  y - 2 = 0 \\
   \Rightarrow y = 2 \\
 \]
By putting y = 3 in equation (4), we have
\[ \Rightarrow x = 10 - 3 = 7\]
By putting y = 2 in equation (4), we have
\[ \Rightarrow x = 10 - 2 = 8\]
So, the coordinates of point D can be (7,3) or (8,2) but coordinates of vertex B are also (8,2). For parallelogram ABCD, any two vertices can never coincide. So, (8,2) is rejected.
The coordinates of point D is (7,3).
According to midpoint theorem, the coordinates of the midpoint of any line joining points (a,b) and (c,d) is given by $\left( {\dfrac{{a + c}}{2},\dfrac{{b + d}}{2}} \right)$
Using the above theorem, the coordinates of the midpoint E of the line joining points D(7,3) and C(9,4) is given by $\left( {\dfrac{{7 + 9}}{2},\dfrac{{3 + 4}}{2}} \right) = \left( {\dfrac{{16}}{2},\dfrac{7}{2}} \right) = \left( {8,\dfrac{7}{2}} \right)$
Also, area of any triangle ADE having vertices A$\left( {{x_1},{y_1}} \right)$, D$\left( {{x_2},{y_2}} \right)$ and E$\left( {{x_3},{y_3}} \right)$ is given by
ar(ADE) = \[\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {{x_1}}&{{x_2}}&{{x_3}} \\
  {{y_1}}&{{y_2}}&{{y_3}} \\
  1&1&1
\end{array}} \right| = \dfrac{1}{2}\left| {{x_1}\left( {{y_2} \times 1 - {y_3} \times 1} \right) - {x_2}\left( {{y_1} \times 1 - {y_3} \times 1} \right) + {x_3}\left( {{y_1} \times 1 - {y_2} \times 1} \right)} \right|\]
$ \Rightarrow $ar(ADE) \[ = \dfrac{1}{2}\left| {{x_1}\left( {{y_2} - {y_3}} \right) - {x_2}\left( {{y_1} - {y_3}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right|{\text{ }} \to {\text{(5)}}\]
By comparing the coordinates, we get
${x_1} = 6,{y_1} = 1,{x_2} = 7,{y_2} = 3,{x_3} = 8,{y_3} = \dfrac{7}{2}$
By putting these above obtained values in the formula given by equation (5), we get
$ \Rightarrow $ar(ADE) = \[\dfrac{1}{2}\left| {6\left( {3 - \dfrac{7}{2}} \right) - 7\left( {1 - \dfrac{7}{2}} \right) + 8\left( {1 - 3} \right)} \right|\]
$ \Rightarrow $ar(ADE) = \[\dfrac{1}{2}\left| {6\left( {\dfrac{{3 \times 2 - 7}}{2}} \right) - 7\left( {\dfrac{{2 - 7}}{2}} \right) + 8\left( { - 2} \right)} \right| = \dfrac{1}{2}\left| {6\left( {\dfrac{{6 - 7}}{2}} \right) - 7\left( {\dfrac{{ - 5}}{2}} \right) - 16} \right|\]
$ \Rightarrow $ar(ADE) = \[\dfrac{1}{2}\left| {6\left( {\dfrac{{ - 1}}{2}} \right) + \dfrac{{35}}{2} - 16} \right| = \dfrac{1}{2}\left| { - 3 + \dfrac{{35}}{2} - 16} \right| = \dfrac{1}{2}\left| {\dfrac{{35}}{2} - 19} \right| = \dfrac{1}{2}\left| {\dfrac{{35 - 19 \times 2}}{2}} \right| = \dfrac{1}{2}\left| {\dfrac{{ - 3}}{2}} \right| = \dfrac{1}{2}\left( {\dfrac{3}{2}} \right) = \dfrac{3}{4}\] sq. units

So, the correct answer is “Option C”.

Note: In this particular problem, we have substituted the value of x i.e., \[x = 10 - y\] in equation (2). Here, we can also substitute this value of x in equation (3) in order to find the values of y. Also, the important step is neglecting the coordinates (8,2) because these coordinates are the same as that of the vertex B of the parallelogram.