Question

A(2,3) and B(-3,4) be two given points. Find the equation of locus of P, so that the area of triangle PAB is 8.5 square units.

Answer 1

- Hint: Assume that the coordinates of the point P be (h,k). Use the fact that area of the triangle $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by $\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} \\
   {{x}_{3}}-{{x}_{1}} & {{y}_{3}}-{{y}_{1}} \\
\end{matrix} \right|$.
Hence find the area of the triangle PAB in terms of h,k. Equate this area to 8.5. Simplify the expression. Replace h by x and k by y to get the equation of the locus of the point P.
Alternatively, note that any such triangle will have the base as AB. Hence find the height h above which the point P must lie from the AB. Hence the locus of P will be two parallel lines to AB at a distance of h from it.


Complete step-by-step solution -

Let P(h,k) be the coordinates of the point P.
We know that area of triangle ABC with $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by $\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} \\
   {{x}_{3}}-{{x}_{1}} & {{y}_{3}}-{{y}_{1}} \\
\end{matrix} \right|$.
In triangle ABP, we have
${{x}_{1}}=2,{{x}_{2}}=-3,{{x}_{3}}=h,{{y}_{1}}=3,{{y}_{2}}=4$ and ${{y}_{3}}=k$
Hence we have
Area of the triangle PAB $=\dfrac{1}{2}\left| \begin{matrix}
   -3-2 & 4-3 \\
   h-2 & k-3 \\
\end{matrix} \right|=\dfrac{1}{2}\left| \begin{matrix}
   -5 & 1 \\
   h-2 & k-3 \\
\end{matrix} \right|=\dfrac{1}{2}\left| -5k+15-h+2 \right|=\dfrac{1}{2}\left| h+5k-17 \right|$
Also, given that the area of triangle PAB is 8.5
Hence we have
$\begin{align}
  & \dfrac{1}{2}\left| h+5k-17 \right|=8.5 \\
 & \Rightarrow \left| h+5k-17 \right|=17 \\
\end{align}$
We know that if $\left| x \right|=y,y>0$, then $x=\pm y$
Hence we have
$h+5k-17=17$ or $h+5k-17=-17$
Hence we have
$h+5k=34$ or $h+5k=0$
Replace h by x and k by y, we get
$x+5y=34$ or $x+5y=0$ which is the locus of P.
Hence the combined equation of locus of P is
$\begin{align}
  & \left( x+5y-34 \right)\left( x+5y \right)=0 \\
 & \Rightarrow {{x}^{2}}+10xy+25{{y}^{2}}-34x-170y=0 \\
\end{align}$
which is the required equation of locus of P.

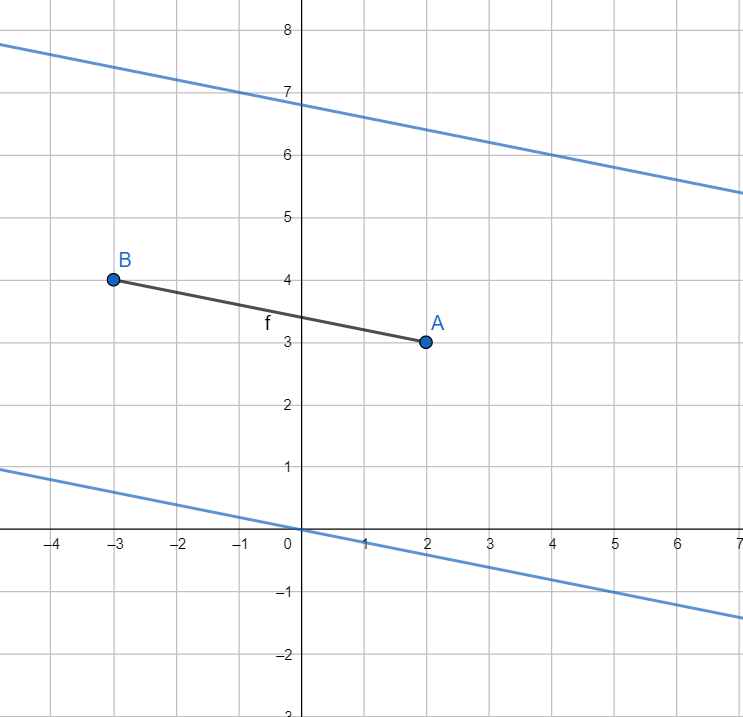
Note: Since the area of triangle PAB is constant and AB is constant in length, we have
Height h above AB at which P must be is also constant. Hence the locus will be two straight lines parallel to AB and at a fixed distance from AB.
Now A (2,3) and B(-3,4). Let h be the distance of point P from AB.
Now, we have
$AB=\sqrt{{{\left( 2+3 \right)}^{2}}+{{\left( 4-3 \right)}^{2}}}=\sqrt{26}$
Hence we have
$\begin{align}
  & \dfrac{1}{2}h\times AB=8.5 \\
 & \Rightarrow h=\dfrac{17}{\sqrt{26}} \\
\end{align}$
Equation of AB in two-point form is given by $y-3=\left( x-2 \right)\dfrac{3-4}{2+3}\Rightarrow 5y+x-17=0$
So let the equation of locus of P be $5y+x+c=0$
Hence we have $\dfrac{\left| c+17 \right|}{\sqrt{25+1}}=\dfrac{17}{\sqrt{26}}\Rightarrow \left| c+17 \right|=17$
Hence we have
$\begin{align}
  & c+17=\pm 17 \\
 & \Rightarrow c=34\text{ or }c=0 \\
\end{align}$
Hence the locus of P is 5y+x+34 = 0 and 5y+x =0, which is the same as obtained above.