Question

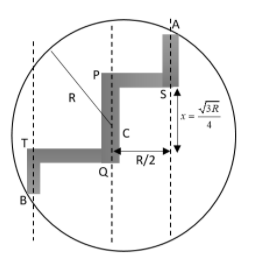
A zigzag tunnel called ASPCQTB is created on earth as represented in the diagram. A particle is released from A and all the collisions will be perfectly inelastic. What will be the time to reach from A to C?

Answer 1

Hint: The acceleration due to gravity can be found by taking the ratio of the volume of the particle, the density of the particle and the gravitational constant to the square of the radius. Here the acceleration of the body will be the product of the acceleration due to gravity and sine of the angle. And the displacement of the body is to be found. From that find the time taken by the body. This will help you in answering this question.

Complete answer:
The acceleration due to gravity can be found by taking the ratio of the volume of the particle, the density of the particle and the gravitational constant to the square of the radius. That is we can write that,
$g=\dfrac{4G\rho \pi {{r}^{3}}}{3{{r}^{2}}}$
That is,
$g=\dfrac{4G\rho \pi r}{3}$
Where $G$ be the gravitational constant, $\rho $ be the density and $r$ be the radius.
Here the acceleration of the body will be the product of the acceleration due to gravity and sine of the angle.
That is,
$a=g\sin \theta $
Substituting the values in it will give,
\[a=\dfrac{4G\rho \pi }{3}\left( r\sin \theta \right)\]
Now we can assume that,
\[r\sin \theta =x\]
That is,
\[a=\dfrac{4G\rho \pi }{3}x\]
As the motion is SHM, the acceleration can be written as,
\[a={{\omega }^{2}}x\]
Comparing this with the equation will give,
\[\omega =\sqrt{\dfrac{4G\rho \pi }{3}}\]
The distance can be shown as,
\[{{x}_{0}}=\dfrac{\sqrt{3R}}{2}\]
Therefore the displacement can be written as,
\[x=\dfrac{\sqrt{3R}}{2}\cos \omega {{t}_{1}}\]
As the value of \[x\] can be written as,
\[x=\dfrac{\sqrt{3R}}{4}\]
Substituting this in the equation will give,
\[\begin{align}
  & \dfrac{\sqrt{3R}}{4}=\dfrac{\sqrt{3R}}{2}\cos \omega {{t}_{1}} \\
 & \therefore {{t}_{1}}=\dfrac{\pi }{3\omega }=\dfrac{T}{6} \\
\end{align}\]
Hence the time has been calculated.

Note:
Simple harmonic motion is a kind of periodic motion in which the restoring force on the object in motion is directly proportional to the magnitude of the displacement of the object and exerts towards the equilibrium position of the object.