Question

A yo-yo is released from your hand with the string wrapped around your finger. If you hold your hand still, the acceleration of the yo-yo is:
A. downward, much greater than g
B. downward, much less than g
C. upward, much less than g
D. upward, much greater than g

Answer 1

Hint:In this question, we need to determine the direction of the acceleration of the yo-yo. For this, we will use Newton’s laws of motion and the relation between the torque, moment of inertia and the acceleration of the body.

Complete step by step answer:
When the yo-yo is released from the hand, then handwork like rigid support, and the wrapped string starts unwrapped so that the yo-yo gain some instant-
-The linear acceleration `a' in a vertically downward direction.
-Angular acceleration $`\alpha '$about its center.
-The force mg works vertically downward.
-The tension T in an upward direction.

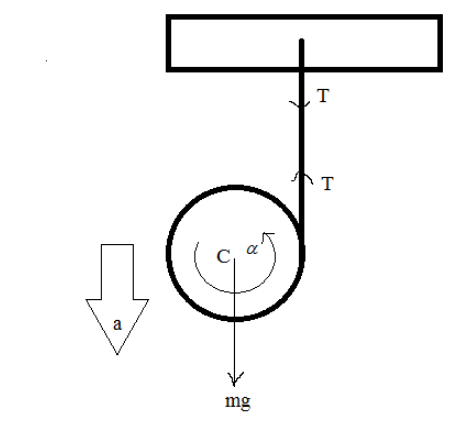
From FBD applying force equation, mg$ - $T$ = $ma …..(i)
Applying torque equation about the center ‘C’, $\tau = I\alpha $
$\Rightarrow T \times R + mg\left( 0 \right) = I\left( {\dfrac{a}{R}} \right)$
$\Rightarrow TR = I\left( {\dfrac{a}{R}} \right)\,\,\,\left[ {\because a = R\alpha } \right]$
$\Rightarrow T = \dfrac{{Ia}}{{{R^2}}}......\left( {ii} \right)$
Putting the value $T = \dfrac{{Ia}}{{{R^2}}}$from equation (ii) into (i)
Therefore, $Mg = \dfrac{{Ia}}{{{R^2}}} = Ma$
$\Rightarrow Mg = Ma + \dfrac{{Ia}}{{{R^2}}}$
$\Rightarrow Mg = \left( {M + \dfrac{{Ia}}{{{R^2}}}} \right)a$
$\Rightarrow a = \dfrac{{Mg}}{{M + \dfrac{I}{{{R^2}}}}} = \dfrac{g}{{1 + \dfrac{I}{{M{R^2}}}}}$
$\Rightarrow a = \dfrac{g}{{1 + \dfrac{I}{{M{R^2}}}}}.......\left( {iii} \right)$
The quantity $\dfrac{I}{{M{R^2}}}$is positive, so the denominator of the equation (iii) would be greater than $1$and hence $a < g$in a downward direction.
As the denominator of the equation (iii) is greater than 1 so, the resultant value of ‘a’ is less than g and is in the downward direction.
Hence, option (B) is correct.

Note:The torque of all the forces is zero, which passes through the point of which the torque has been computed. When a force is applied to the body, not only the applied force is acting, there are many other forces like a gravitational force. For example frictional force f and the normal force N that balances the other force. Therefore in the force equation
$\Rightarrow {\overrightarrow F _{net}} = m\overrightarrow a ,$
$\Rightarrow {\overrightarrow F _{net}} = $The vector sum of all the forces
$\Rightarrow {\overrightarrow F _{net}} = {\overrightarrow F _{ex + }} + \overrightarrow F g + \overrightarrow f + \overrightarrow N $