
A young man rides his motorcycle at $ 25\,kmh{r^{ - 1}} $ , he has to spend $ Rs.2\, $ per $ km $ on petrol; if he rides his motorcycle at $ 40\,kmh{r^{ - 1}} $ he has to spend $ Rs.5 $ per $ km $ on petrol. He has \[Rs.100\] to spend on petrol and wishes to find the maximum distance he can travel within one hour. Express this as a linear programming problem.
Answer
561.9k+ views
Hint: In this question, we need to determine the maximum distance he can travel in one hour. We will determine $ Z $ and then determine subject to constraints using given. Then plot it graphically to determine the corner points and check objective function at end points when $ Z = \left( {x + y} \right)\,km $ and by which we will determine the maximum distance he can travel in one hour.
Complete step-by-step answer:
Consider when the speed is $ 25\,kmh{r^{ - 1}} $ the man travels $ x\,km $
Also, when the speed is $ 40\,kmh{r^{ - 1}} $ the man travels $ y\,km $ .
Therefore, the total distance travelled is given by $ Z = \left( {x + y} \right)\,km $
Now, it is given that the man has \[Rs.100\] to spend on petrol.
Thus, total cost = $ 2x + 5y \leqslant 100 $
Now, the time taken to travel $ x\,km $ at the speed of $ 25\,kmh{r^{ - 1}} $ = $ \dfrac{x}{{25}}\,hr $
Then, time taken to travel $ y\,km $ at the speed of $ 40\,kmh{r^{ - 1}} $ = $ \dfrac{y}{{40}}\,hr $
Now, it is given that the maximum time is $ 1\,hour $ .
Therefore,
$ \dfrac{x}{{25}} + \dfrac{y}{{40}} \leqslant 1 $
$ \dfrac{{40x + 25y}}{{1000}} \leqslant 1 $
$ 40x + 25y \leqslant 1000 $
$ 5\left( {8x + 5y} \right) \leqslant 5\left( {200} \right) $
$ 8x + 5y \leqslant 200 $
So, $ x \geqslant 0 $ and $ y \geqslant 0 $ .
Thus, we have to Maximize $ Z = \left( {x + y} \right)\,km $ .
Subject to the constraints:
$ 2x + 5y \leqslant 100 $
Let it be equation (1)
$ 8x + 5y \leqslant 200 $
Let it be equation (2)
$ x \geqslant 0 $ ; $ y \geqslant 0 $
Let this be (3)
Now we can solve graphically,
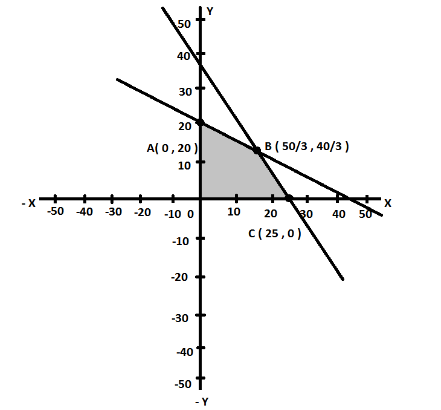
The shaded region shows feasible regions which are determined by the above system of constraints.
Therefore, the points of the feasible region are $ O\left( {0,0} \right) $ , $ A\left( {0,20} \right) $ , $ B\left( {\dfrac{{50}}{3},\dfrac{{40}}{3}} \right) $ and $ C\left( {25,0} \right) $ .
Hence, the maximum distance that the man can travel in $ 1\,hour $ is $ 30\,km $ .
Now, let us check the objective function at the end points,
Here, the distance travelled by him at the speed of $ 25\,kmh{r^{ - 1}} $ is $ \dfrac{{50}}{{3\,}}\,km $ , and the distance travelled by him at the speed of $ 40\,kmh{r^{ - 1}} $ is $ \dfrac{{40}}{3}\,km $ .
Note: In this question, it is important to note here that in these types of questions be careful while forming subject to constraints. Also, note carefully what has been asked i.e., to maximize or minimize
$ Z $ . And by plotting we can get corner points, then apply in $ Z $ and determine minimum or maximum value.
Complete step-by-step answer:
Consider when the speed is $ 25\,kmh{r^{ - 1}} $ the man travels $ x\,km $
Also, when the speed is $ 40\,kmh{r^{ - 1}} $ the man travels $ y\,km $ .
Therefore, the total distance travelled is given by $ Z = \left( {x + y} \right)\,km $
Now, it is given that the man has \[Rs.100\] to spend on petrol.
Thus, total cost = $ 2x + 5y \leqslant 100 $
Now, the time taken to travel $ x\,km $ at the speed of $ 25\,kmh{r^{ - 1}} $ = $ \dfrac{x}{{25}}\,hr $
Then, time taken to travel $ y\,km $ at the speed of $ 40\,kmh{r^{ - 1}} $ = $ \dfrac{y}{{40}}\,hr $
Now, it is given that the maximum time is $ 1\,hour $ .
Therefore,
$ \dfrac{x}{{25}} + \dfrac{y}{{40}} \leqslant 1 $
$ \dfrac{{40x + 25y}}{{1000}} \leqslant 1 $
$ 40x + 25y \leqslant 1000 $
$ 5\left( {8x + 5y} \right) \leqslant 5\left( {200} \right) $
$ 8x + 5y \leqslant 200 $
So, $ x \geqslant 0 $ and $ y \geqslant 0 $ .
Thus, we have to Maximize $ Z = \left( {x + y} \right)\,km $ .
Subject to the constraints:
$ 2x + 5y \leqslant 100 $
Let it be equation (1)
$ 8x + 5y \leqslant 200 $
Let it be equation (2)
$ x \geqslant 0 $ ; $ y \geqslant 0 $
Let this be (3)
Now we can solve graphically,

The shaded region shows feasible regions which are determined by the above system of constraints.
Therefore, the points of the feasible region are $ O\left( {0,0} \right) $ , $ A\left( {0,20} \right) $ , $ B\left( {\dfrac{{50}}{3},\dfrac{{40}}{3}} \right) $ and $ C\left( {25,0} \right) $ .
Hence, the maximum distance that the man can travel in $ 1\,hour $ is $ 30\,km $ .
Now, let us check the objective function at the end points,
| CORNER POINTS | Z=x+y |
| O(0,0) | 0 |
| A(0.20) | 20 |
| B($\dfrac{50}{3}$ ,$\dfrac{40}{3}$) | 30 |
| C(25,0) | 25 |
Here, the distance travelled by him at the speed of $ 25\,kmh{r^{ - 1}} $ is $ \dfrac{{50}}{{3\,}}\,km $ , and the distance travelled by him at the speed of $ 40\,kmh{r^{ - 1}} $ is $ \dfrac{{40}}{3}\,km $ .
Note: In this question, it is important to note here that in these types of questions be careful while forming subject to constraints. Also, note carefully what has been asked i.e., to maximize or minimize
$ Z $ . And by plotting we can get corner points, then apply in $ Z $ and determine minimum or maximum value.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE





