Question

(a) Write the necessary condition for the phenomenon of total internal reflection to occur.
(b) Write the relation between the refractive index and critical angle for a given pair of optical media.

Answer 1

Hint: Study about the reflection and refraction and the relations between the angle of incidence and the angle of refraction. Try to understand what total internal reflection means and at what point it will happen.

Complete Step-by-Step solution:
(a) Reflection can be defined as the change in direction of the light beam in the interface of two media where the beam returns to the original medium.
When a light beam travels through an optically denser medium to a rarer medium a part of the light beam gets reflected to the denser medium and the other part is refracted to the rarer medium. This reflection is called the internal reflection.
Now if we keep on increasing the angle of incidence of the light beam at the interface of the two media after a certain angle refraction is not possible and the light beam is totally deflected. This process is called the total internal reflection.
This angle of incidence at which angle of refraction will be ${{90}^{0}}$ is called the critical angle. Only if the angle of incidence is greater than the critical angle than we can obtain total internal reflection.
So, the necessary condition for total internal reflection is that the angle of incidence should be greater than the critical angle.

(b) Consider the angle of incidence is equal to the critical angle.
$i={{i}_{c}}$
Where, i is the angle of incidence and ${{i}_{c}}$ is the critical angle.

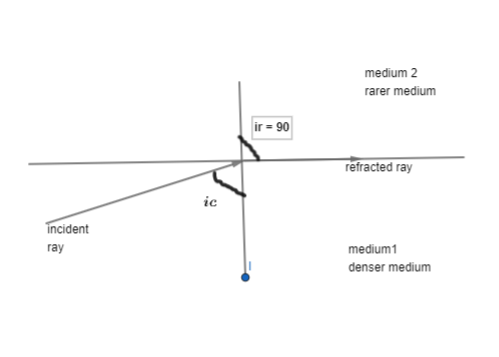
At this condition angle of refraction will be ${{i}_{r}}={{90}^{0}}$
From Snell's law we can write that,
$\dfrac{\sin i}{\sin {{i}_{r}}}={{n}_{21}}=\dfrac{1}{{{n}_{12}}}$
Where, ${{n}_{21}}$ is the refractive index of the rarer medium with respect to the denser medium and ${{n}_{12}}$ is the refractive index of the denser medium with respect to the rarer medium.
Now,
$\begin{align}
  & \dfrac{\sin {{i}_{c}}}{\sin {{i}_{r}}}={{n}_{21}}=\dfrac{1}{{{n}_{12}}} \\
 & \dfrac{\sin {{i}_{c}}}{\sin {{90}^{0}}}={{n}_{21}}=\dfrac{1}{{{n}_{12}}} \\
 & \sin {{i}_{c}}={{n}_{21}}=\dfrac{1}{{{n}_{12}}} \\
\end{align}$
This is the relation between the critical angle and the refractive index.

Note: For total internal reflection to happen the light beam should always travel from the denser medium to the rarer medium. Because when light beam goes from rarer to denser medium the refracted ray will go towards the normal at the interface and we will never get an angle of refraction of ${{90}^{0}}$ and hence we will not get total internal reflection.