Question

A wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

Answer 1

Hint: You could firstly represent the given situation in a neat diagram. Now take the displacement of the plank as x then, the displacement of the man will be 10-x. Then, you could recall the expression for net displacement of the system, and then substituting accordingly will give you the required displacement.

Formula used:
The net displacement of the system,
$S=\dfrac{{{m}_{1}}{{r}_{1}}+{{m}_{2}}{{r}_{2}}}{{{m}_{1}}+{{m}_{2}}}$

Complete step-by-step solution
In the question, we are given a 20kg wooden plank that lies on a smooth floor. A 60kg man walks across this plank of 10m. We are asked to find the displacement of the plank over the floor as the man reaches the other end of the plank. So the situation is as represented below,

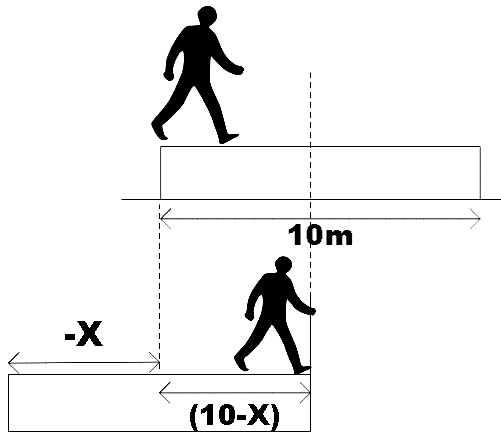
As the floor is smooth, there will be no friction, also, there is no mention of any external force, so, the net displacement of the center of mass should be zero.
We know that the net displacement of the center of mass of the system is given by,
$S=\dfrac{{{m}_{1}}{{r}_{1}}+{{m}_{2}}{{r}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
Here, ${{m}_{1}}$ is the mass of the plank, ${{m}_{2}}$ is the mass of the man, ${{r}_{1}}$ is the displacement of the scale and ${{r}_{2}}$ is the displacement of the man.
Substituting according gives,
$S=\dfrac{20\times \left( -x \right)+60\times \left( 10-x \right)}{20+60}$
But, net displacement of the centre of mass of the system is zero here, so,
$\dfrac{20\times \left( -x \right)+60\times \left( 10-x \right)}{20+60}=0$
$\Rightarrow -20x+600-60x=0$
$\Rightarrow 80x=600$
$\therefore x=\dfrac{600}{80}=7.5m$
Therefore, the displacement of the plank over the floor when the man reaches the other end of the plank is found to be 7.5m.

Note: If you are wondering why we have taken negative signs for the displacement of the plank, it is to symbolize the displacement of the plank opposite to the displacement of man. Relating the situation to some real-life experience you will realize that this is exactly what happens in such a situation. Hence the negative sign.