Question

A wooden plank is placed over a pit that is $L = 5.00 m$ wide. A physics student stands in the middle of the plank and begins to jump up and down such that she jumps upward from the plank two times each second. The plank oscillates with a large amplitude, with maximum amplitude at its centre. What is the speed of transverse waves, v, on the plank?

Answer 1

Hint : Given the length of wooden plank and the frequency of the wave. First, we consider this case as a fundamental note. We will evaluate the wavelength of the wave. Then, we will find the velocity of the transverse wave by the wavelength multiplied to the frequency.

Complete step-by-step solution:
Given the length of the wooden plank, $L = 5.00 m$
A student stands in the middle of the plank and begins to jump up and down. It indicates it is a fundamental note.

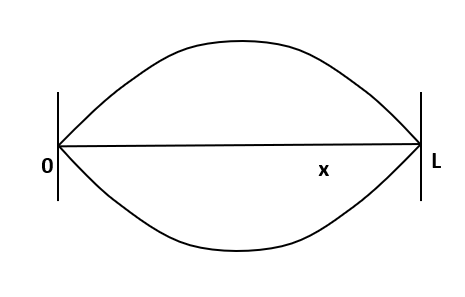
Here, the wavelength is equal to twice the length.
$\lambda = 2L$
So, we get wavelength after putting the value of length.
$\lambda = 2 \times 5 = 10 m$
The frequency is the number of oscillations in a second.
Frequency, $f = 2Hz$
The speed is defined as the product of wavelength and the frequency.
$v = \lambda f$
Now put the values of wavelength and frequency.
$v = 10 \times 2 = 20 ms^{-1}$
The speed of transverse waves, v, on the plank is $20 ms^{-1}$.

Note: A transverse wave is a traveling wave whose vibrations are perpendicular to the direction of the flow. A simple illustration of the wave can be formed on a horizontal length of the string by adjusting one end of the string and moving the other upward and downward. Light is another illustration of a transverse wave, where the vibrations are electric and magnetic fields that are perpendicular to the ideal light waves that describe the propagation direction.