Question

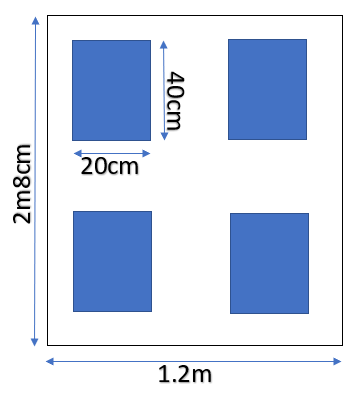
A wooden door, 2m 8cm high and 1.2m wide has 4 glass panes fitted on it. Each pane is 40cm by 20cm, what is the area of the wood?

Answer 1

Hint: In this question we are given the dimension of rectangular wooden door and dimension of rectangular glass panes. We can find the area of wood by subtracting the area of glass panes from the area of the door using the formula of area of rectangle = ${\text{length}} \times {\text{breadth}}$.

Complete step-by-step answer:
First, we have to convert all measurements either in meter or in centimeter
So, Height of wooden door $ = 2m8cm = 2 \times 100 + 8 = 208cm{\text{ [}}\because {\text{1m = 100cm]}}$
Width of wooden door = $1.2m = 1.2 \times 100 = 120cm$

Area of wooden door
$
   = 208 \times 120 \\
   = 24960c{m^2} \\
$
Length of glass pane = $40cm$
Width of glass pane = $20cm$


Area of one glass pane
$
   = 40 \times 20 \\
   = 800c{m^2} \\
$
Area of wood = Area of Wooden door – Area of 4 glass pane
$
   = 24960 - 4 \times 800 \\
   = 24960 - 3200 \\
   = 21769c{m^2} \\
  or \\
   = \dfrac{{21760}}{{10000}}{m^2}{\text{ }}\left[ {\because 1{m^2} = 10000c{m^2}} \right] \\
   = 2.176{m^2} \\
$

Therefore, the area of wood is $2.176{m^2}$

Note: In order to solve such types of problems students must remember the area of basic geometrical figures and also extra care must be taken for practical problems in order to remove some parts of the area from the figure.