Question

A wooden cube of side 10 cm and specific gravity $0.8$ floats in water with its upper surface horizontal. What depth of the cube remains immersed ? What mass of aluminium of specific gravity $2.7$ must be attached to
(i) The upper surface
(ii) The lower surface so that the cube will be just immersed ?

Answer 1

Hint:To calculate depth immersed, use buoyancy $ = $ weight of cube
For point (i), buoyant force will only be applied on the cube and weight would increase.
Buoyancy $ = $ volume of cube $ \times $ density of water $ \times $ g $ = $ total weight
For point (ii), buoyant force will be applied both on cube and aluminium mass and weight would increase too.
Buoyancy $ = ($volume of cube $ + $ volume of aluminium$) \times $ density of water $ \times $ g $ = $ total weight
Using the above concept we can solve this problem.

Complete step by step answer:
For calculating the depth of the cube immersed in water. Let x be the depth of the cube remains immersed in water therefore,
Volume of cube $(V) = {a^3}$
Where
a $ = $ side of cube
given that $a = 10cm = 0.1m$
$a = {10^{ - 1}}m$
So, volume of cube
\[
{V_C} = {a^3} \\
\Rightarrow
{V_C} = {({10^{ - 1}})^3} \\
\Rightarrow
{V_C} = {10^{ - 3}}{m^3} …..(1) \\\]
Now, the volume of cube inside the water is
\[
{V_w} = x{a^2} = {({10^{ - 1}})^2}x \\
\Rightarrow
{V_w} = {10^{ - 2}}x{m^3} …..(2) \\
\]
Let the density of the cube be ${\rho _C}$ and the density of water be ${\rho _W}$.
So, weight of cube $ = $ density of cube $ \times $ volume of cube $ \times $ g
From equation 1
\[
{W_C} = {\rho _S}{V_C}g \\
\Rightarrow
{W_C} = {\rho _C}{a^3}g …..(3) \\
\]
Now, the buoyant force on cube is
$
{F_B} = {\rho _W}{V_W}g …..(4) \\
$
$\Rightarrow{F_B}$ = Weight of cube = ${W_C}$ (from free body diagram of cube)

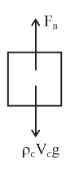
Free body diagram of cube
So,
\[
{\rho _W}{V_W}g = {\rho _C}{V_C}g \\
\Rightarrow
\dfrac{{{\rho _C}}}{{{\rho _W}}} = \dfrac{{{V_W}}}{{{V_C}}} \\
\]
Given that specific gravity
\[
\dfrac{{{\rho _C}}}{{{\rho _W}}} = 0.8 …..(5) \\
So, \dfrac{{{V_W}}}{{{V_C}}} = 0.8 \\\] From equation 1
${V_C} = {10^{ - 3}}{m^3} \\
\Rightarrow{V_W} = 0.8 \times {10^{ - 3}}{m^3} \\$ From equation 2
$\Rightarrow{V_W} = {10^{ - 2}}x \\
\Rightarrow{10^{ - 2}}x = 0.8 \times {10^{ - 3}} \\
\Rightarrow x = \dfrac{{0.8 \times {{10}^{ - 3}}}}{{{{10}^{ - 2}}}} \\
\Rightarrow x = 0.8 \times {10^{ - 1}} \\
\Rightarrow x = 0.08m \\
\therefore x = 8cm \\
$
Hence, the depth of the cube that is immersed in water is 8 cm.
(i) Let m be the mass of aluminium that is attached to the upper surface. So that cube is just immersed in water.
Therefore,

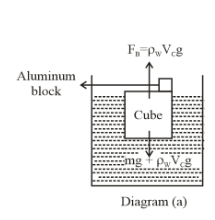
From diagram a
\[
{\rho _C}{V_C}g + mg = {\rho _W}{V_C}g \\
\]
From diagram a
\[
{\rho _C}{V_C} + m = {\rho _W}{V_C} \\
\Rightarrow
{\rho _C} + \dfrac{m}{{{V_C}}} = {\rho _W} \\
\Rightarrow
\dfrac{m}{{{V_C}}} = {\rho _W} - {\rho _C} \\
\Rightarrow
m = {V_C}({\rho _W} - {\rho _C}) …..(6) \\
\]
Here ${\rho _W}$ =density of water = $1000kg/{m^3}$
\[{\rho _C} = 0.8{\rho _W} \\
\Rightarrow{\rho _C} = 0.8 \times 1000 \\
\Rightarrow{\rho _C} = 800kg/{m^3} \\
\Rightarrow{V_C} = {10^{ - 3}}{m^3} \\
\] from equation 1
On putting the values of ${\rho _C},{V_C}$ and ${\rho _W}$ in equation 6
\[
m = {10^{ - 3}}(1000 - 800) \\
\Rightarrow m = 200 \times {10^{ - 3}} \\
\Rightarrow m = 2 \times {10^{ - 1}}kg \\
\Rightarrow m = 200gm \\
\]
(ii) Let the mass of the aluminium block be m i.e., attached to the lower surface of the cube. So, that cube is just immersed in water.

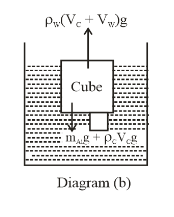
From diagram b
The volume of the aluminium block is ${V_{Al}}$. Therefore
$
{V_{Al}} = \dfrac{m}{{{\rho _{Al}}}} …..(7) \\
$
${\rho _{Al}}$ = density of aluminium
So, from diagram b, we have
\[
(m + {\rho _C}{V_C})g = {\rho _W}({V_C} + {V_{Al}})g \\
\Rightarrow
m + {\rho _C}{V_c} = {\rho _W}\left( {{V_C} + \dfrac{m}{{{\rho _{Al}}}}} \right) \\
\] from equation 7
\[
\Rightarrow
m + {\rho _C}{V_C} = {\rho _W}{V_C} + \dfrac{{{\rho _W}m}}{{{\rho _{Al}}}} \\
\Rightarrow
m - m\left( {\dfrac{{{\rho _W}}}{{{\rho _{Al}}}}} \right) - {\rho _W}{V_C} - {\rho _C}{V_C} \\
\Rightarrow
m\left[ {1 - \dfrac{{{\rho _W}}}{{{\rho _{Al}}}}} \right] = ({\rho _W} - {\rho _C}){V_C} …..(8) \\
\]
Given, the specific gravity of aluminium
\[
\dfrac{{{\rho _{Al}}}}{{{\rho _W}}} = 2.7 \\
\]
So,
\[m\left( {1 - \dfrac{1}{{2.7}}} \right) = ({\rho _W} - {\rho _C}){V_C} \\
\Rightarrow {\rho _W} = 1000kg/{m^3} \\
\Rightarrow
{\rho _C} = 800kg/{m^3} \\
\Rightarrow
{V_C} = {10^{ - 3}}{m^3} \\
\]
So,
\[
m\left( {\dfrac{{2.7 - 1}}{{2.7}}} \right) = (1000 - 800) \times {10^{ - 3}} \\
\Rightarrow
m\left( {\dfrac{{1.7}}{{2.7}}} \right) = 200 \times {10^{ - 3}} \\
\Rightarrow
m = \dfrac{{200 \times 2.7 \times {{10}^{ - 3}}}}{{1.7}} \\
\Rightarrow
m = \dfrac{{27 \times 2 \times {{10}^{ - 1}}}}{{17}} \\
\Rightarrow
m = \dfrac{{54}}{{17}} \times {10^{ - 1}} \\
\Rightarrow
m = 3.1764 \times {10^{ - 1}}kg \\
\therefore
m = 317.64gm \\
\]
Hence, the $317.64gm$ of aluminium block should be attached at the lower surface. So that the cube will be just immersed.

Note: In order to solve these types of problems, students must understand about the buoyancy force i.e,the upward force that a fluid exerts on an object that is less dense than itself.Buoyancy allows a boat to float on water and provides lift for balloons.
Specific gravity is also called relative density i.e., the ratio of the density of a substance to that of a standard substance. Generally most of the time the density of substance is compared with density of water.
Specific density $ = \dfrac{{density\,of\,substance}}{{density\,of\,water}}$