Question

A wooden cube is painted with purple on all the four adjoining faces and yellow on two opposite faces and then it is into \[216\] identical smaller cubes then how many cubes are there having two different colour on them
a) \[24\]
b) \[20\]
c) \[40\]
d) \[48\]

Answer 1

Hint: Since we are given a bigger cube whose four adjoining faces are purple and two opposite faces are yellow and it is divided into \[216\] identical smaller cubes, that means each corner has \[6\] cubes. We can get two different colours only on the corners of the two opposite faces, as we get colours on two faces of cubes on all corners but adjacent face corner cubes have the same colours. So we count them to reach the result.

Complete step-by-step answer:
Since our bigger cube is divided into \[216\] identical smaller cubes, that means \[{6^3}\] identical smaller cubes. That means each corner has 6 cubes. But the cubes on the edges get their three faces coloured, but only two different colors. Hence we count all the cubes on edges and corners of opposite faces of the bigger cube.

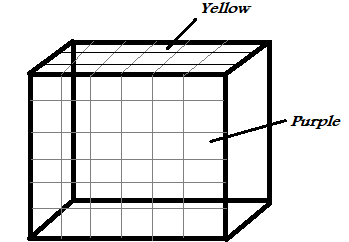
On four sides of opposite faces, each side has 6 cubes. But each of the four cubes on edges are counted twice, so we subtract four from each both the faces
Cubes with two colours are \[(6 + 6 + 6 + 6) - 4 = 20\]
As there are two such cubes, we have \[20 \times 2 = 40\] cubes having two different colours on them.

So, the correct answer is “Option c”.

Note: We have to be careful while solving such questions as there are great chances that we may count a cube two times or we may forget to count a cube. It was important to subtract four from each both the faces as we had counted four of the cubes twice. Each face contains \[6 \times 6 = 36\] identical cubes.