Question

A wooden box with a lid is made of 2.5 cm thick wood. Inner length, breadth and height of the box are 1 m, 65 cm and 55 cm. Find the total expenditure of colouring its outer surface area at the rate of 15 per square meter.

Answer 1

Hint: First, before solving this question, we must draw the diagram of the figure with inner dimensions as length, breadth and height of the box are 1 m, 65 cm and 55 cm respectively. Then, for the outer length we can see that the units are in the meter and we are having all other units in centimetre so we get the inner length value as 1m=100cm. Then, we can see that the outer length is the sum of the inner length with twice the thickness and similarly breadth and height is calculated. Then, by applying the formula for the total surface area for outer dimensions with formula as $ S=2\left( lb+bh+hl \right) $ and multiplying it with cost rate of 15, we get the final answer.

Complete step-by-step answer:
In this question, we are supposed to find the total expenditure of colouring its outer surface area at the rate of 15 per square meter of the wooden box with lid over it and has a thickness of 2.5 cm.
So, before solving this question, we must draw the diagram of the figure with inner dimensions as length, breadth and height of the box are 1 m, 65 cm and 55 cm respectively.

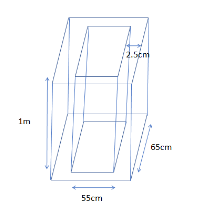
Now, from the above drawn figure, we can easily calculate the value of the outer length, breadth and height.
So, for the outer length we can see that the units are in the meter and we are having all other units in centimetre so we get the inner length value as:
Inner length=1m=100cm
Now, we can see that the outer length is sum of the inner length with the twice of the thickness as:
Outer length= $ 100+2\times 2.5 $
Outer length=100+5=105
Similarly, we can have the same concept for the outer breadth and outer height as:
Outer breadth=65+5=70
Outer height=55+5=60
So, now by using the formula for the outer surface S of the cuboid which is a wooden box with length as 105 cm, breadth as 70cm and height as 60 cm as:
 $ S=2\left( lb+bh+hl \right) $
So, the outer surface area after substitution is:
 $ \begin{align}
  & S=2\left( 105\times 70+70\times 60+60\times 105 \right) \\
 & \Rightarrow S=2\left( 7350+4200+6300 \right) \\
 & \Rightarrow S=2\times 17850 \\
 & \Rightarrow S=35700c{{m}^{2}} \\
\end{align} $
Now, to get the cost in per meter square, we need to convert it into meter square by dividing it by 10000 as:
 $ \begin{align}
  & S=\dfrac{35700c{{m}^{2}}}{10000} \\
 & \Rightarrow S=3.57{{m}^{2}} \\
\end{align} $
So, now to get the cost of colouring the outer surface area at the rate of 15 per square metre, we need to multiply 15 with 3.57 to get the value as:
 $ 3.57\times 15=53.55 $
So, the total cost of colouring the outer surface area of the wooden box is Rs. 53.55.
Hence, the answer is Rs. 53.55.

Note: Now, to solve these types of questions we need to know some of the basic conversions beforehand so that we can easily proceed in these types of questions. Then, some of the basic conversions are:
 $ \begin{align}
  & 1m=100cm \\
 & 1cm=\dfrac{1}{100}m \\
\end{align} $
Moreover, we must be careful while applying the formula for the total surface area of the cuboid as most of times it get mixed with the curved surface area of the cuboid as:
 $ \begin{align}
  & TSA=2\left( lb+bh+hl \right) \\
 & CSA=2\left( l+b \right)h \\
\end{align} $ .