Question

A wooden block of mass 10 g is dropped from a tower 100m high. Simultaneously, a bullet of mass 10g is fired from the foot of the tower vertically upwards with a velocity of 100m/s. If the bullet is embedded in it, how high will the block rise above the top of the tower before it starts falling? ($g = 10m/{s^2}$)
(a) 75m
(b) 85m
(c) 80m
(d) 10m

Answer 1

Hint: According to the law of conservation of momentum, initial momentum of a system before collision is equal to the final momentum after collision.

Formula Used:
Equations of motion:
$y = ut + \dfrac{1}{2}a{t^2}$ …… (1)
$v = u + at$ …… (2)
${v^2} - {u^2} = 2ay$ …… (3)
where,
y is the distance covered by a particle in vertical direction.
u is initial velocity.
a is constant acceleration
t is time taken to cover y distance.
Conservation of momentum for bodies which stick together after collision:
${m_1}{v_1} + {m_2}{v_2} = ({m_1} + {m_2})V$ …… (4)
where,
${m_1}$is the mass of the 1st body.
${m_2}$is the mass of the 2nd body.
${v_1}$ is the velocity of the 1st body before collision.
${v_2}$is the velocity of the 2nd body before collision.
V is the combined velocity after collision.

Complete step by step answer:

Given:
1. Mass of wooden block (${m_1}$) = 10g
2. Mass of bullet (${m_2}$) = 10g
3. Initial velocity of wooden block (${u_1}$) = 0m/s
4. Initial velocity of bullet (${u_2}$) = 100 m/s.
5.Height of tower = 100m

To find: The height covered by the bullet-block system after collision before it starts to fall again.

Rough sketch:

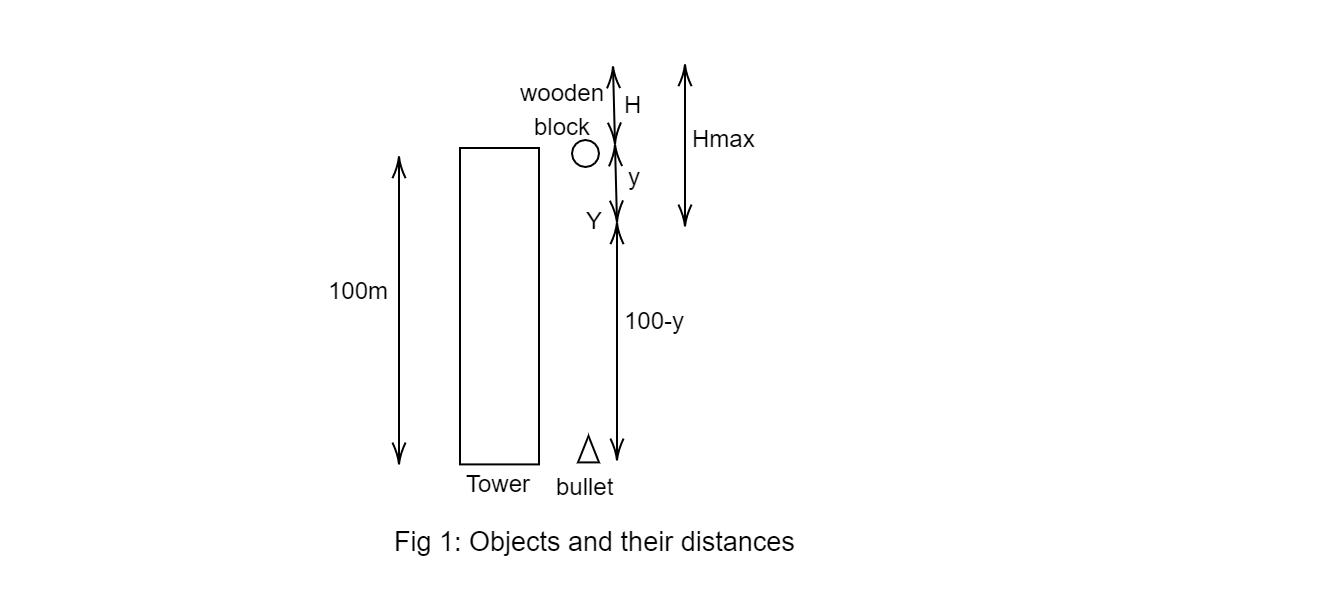
Step 1 of 4:
Take the foot of the tower as its origin. Let the bullet and block collide at point Y after time t which is at distance y from the top of the tower.
Find distance y using eq (1) for wooden block:
$y = 0 + \dfrac{1}{2} \times 10 \times {t^2}$
$y = 5{t^2}$ …… (5)
Find distance y using eq (1) for bullet:
$100 - y = 100t - \dfrac{1}{2} \times 10 \times {t^2}$
$y = 5{t^2} - 100t + 100$ …… (6)
Solving eq (5) and (6) gives: $y = 5m$ and $t = 1s$.

Step 2 of 4:
Let the velocities of wooden block and bullet just before collision be ${v_1}$ and ${v_2}$ respectively.
Find ${v_1}$ using eq (2):
${v_1} = 0 + 10 \times 1$
${v_1} = 10m/s$
Find ${v_2}$ using eq (2):
${v_2} = 100 - 10 \times 1$
${v_2} = 90m/s$

Step 3 of 4:
Find the combined velocity after collision using eq (4):
$
   - 10 \times 10 + 10 \times 90 = 2 \times 10 \times V \\
  V = 40m/s \\
 $

Step 4 of 4:
Find the height covered by the bullet-block system using eq (3):
$
  0 - {40^2} = 2( - 10){H_{\max }} \\
  {H_{\max }} = 80m \\
 $
Here, ${H_{\max }}$is the distance covered in vertical direction from the point Y.
Find the distance covered above the tower by subtracting y from ${H_{\max }}$:
$
  H = {H_{\max }} - y \\
  H = 80 - 5 \\
  H = 75m \\
 $

Correct Answer: Height by which the block will rise above the tower: (a) 75m.

Note: In questions where we have to find the distance travelled after collision, first find the velocities of bodies before collision. Apply conservation of momentum and then find the distance covered by the combined body using equations of motion.