Question

A wooden block is floating on water kept in the beaker. 40% of the block is above the water surface. Now the beaker is kept inside a lift that starts going upward with acceleration equal to g/2. The block will then,
$\left( A \right)$ Sink
$\left( B \right)$ Float with 10% above the water surface
$\left( C \right)$ Float with 40% above the water surface
$\left( D \right)$ Float with 70% above the water surface

Answer 1

- Hint: In this use the concept of Archimedes’ principle i.e. weight of wooden block is equal to the weight of liquid displaced and later on in the solution use the concept when this arrangement is taken into the lift the net acceleration working on the block is the sum of acceleration by which the lift is moving in the upward direction and the acceleration due to Earth’s gravity so use these concepts to reach the solution of the question.

Complete step-by-step answer:

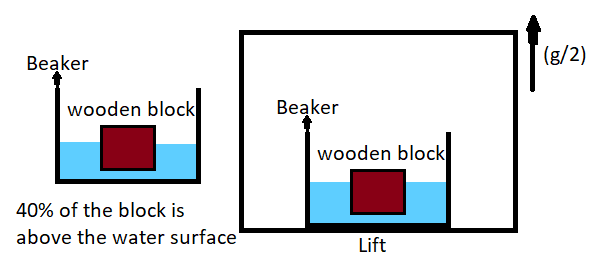
Now it is given that 40% of the block is above the surface, therefore 60% of the block is inside the liquid.
Therefore %volume which is inside the liquid = 60%.
So the water displaced by the wooden block = $\left( {\dfrac{{60}}{{100}}} \right)V{\rho _L}g$.
Where V = total volume of the wooden block, ${\rho _L}$ = density of the liquid and g = Earth’s gravity.
Now the weight of the wooden block is mass times the Earth’s gravity (g) = mg.
So according to Archimedes’ principle,
Weight of wooden block = weight of liquid displaced
$ \Rightarrow mg = \left( {\dfrac{{60}}{{100}}} \right)V{\rho _L}g$ ..................... (1)
Now when this arrangement was kept in the lift and lift is going upwards with acceleration = (g/2).
So the net acceleration working on the wooden block = (g + g/2) = 3g/2.
So the weight of the wooden block becomes = 3mg/2.
Now let the water displaced by the wooden block at this time = ${V_f} \times {\rho _L} \times g$
Where ${V_f}$= fraction of volume of wooden block inside the liquid, ${\rho _L}$ = density of the liquid and g = Earth’s gravity.
So according to Archimedes’ principle,
Weight of wooden block = weight of liquid displaced
$ \Rightarrow \dfrac{{3mg}}{2} = {V_f}{\rho _L}g$
Now from equation (1) we have,
$ \Rightarrow \dfrac{{3\left( {\dfrac{{60}}{{100}}} \right)V{\rho _L}g}}{2} = {V_f}{\rho _L}g$
Now simplify the above equation we have,
$ \Rightarrow {V_f} = \dfrac{{3\left( {\dfrac{{60}}{{100}}} \right)V}}{2} = \dfrac{9}{{10}}V = 0.9V = $90% of V
So 90 % of the wooden block is inside the liquid.
So 100 – 90 = 10 % of the wooden block is above the water surface.
So this is the required answer.
So the block will float with 10% above the water surface.
Hence option (B) is the correct answer.

Note: Whenever we face such types of questions the key concept involved in this is that the weight of the wooden block is equal to the weight of the liquid displaced so first calculate the mass of the wooden block according to given condition as above then the net acceleration working on the block is increased as the lift is going upward and if the lift going downward the net acceleration working on the wooden block is decreased so when the beaker is in the lift developed the equation as above and simplify, we will get the required answer.