
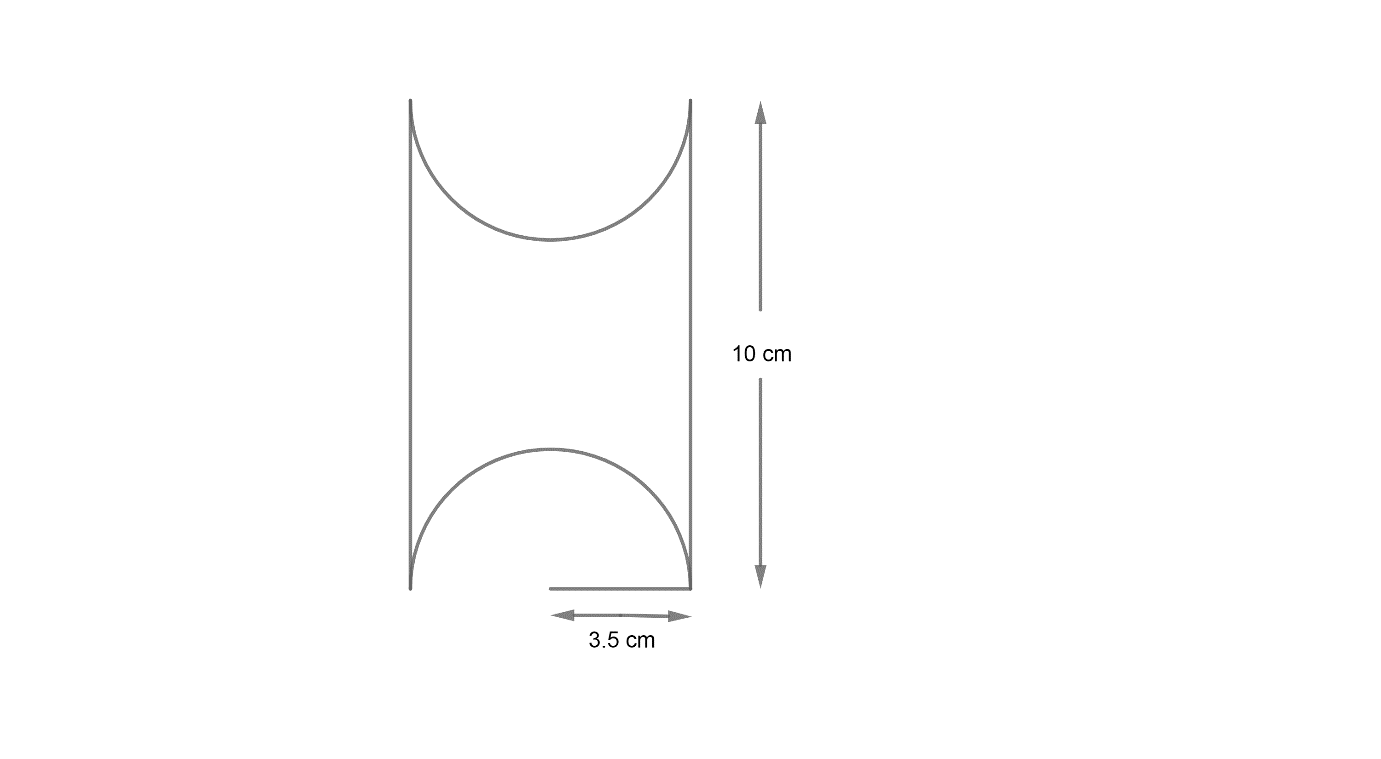
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10cm, and its base is of radius 3.5cm, find the total surface area of the article.

Answer
531.5k+ views
Hint: As the article was made by scooping out a hemisphere from each end of a solid cylinder, then the total surface area of the article would be the sum of the curved surface area of the cylinder and twice of the curved surface area of the hemisphere.
That is,
TSA of article = curved surface area of cylinder + 2 $\times $ curved surface area of hemisphere.
We will be using the below formulas.
The formula for the CSA of cylinder $=2\pi rh\ sq.unit$
The formula for the CSA of hemisphere $=2\pi {{r}^{2}}\ sq.unit$
Complete step-by-step answer:
Let us consider the figure as shown,
Here, we have been given the height of the cylinder as h = 10cm and the radius of the cylinder is given as r = 3.5 cm.
Now, we can say that since the hemisphere is scooped out from the cylinder, the radius of the hemisphere will be the same as the radius of the cylinder.
Hence, we get the radius of the hemisphere = 3.5 cm.
Now, we have to compute the total surface area (TSA) of article = the curved surface area of cylinder + 2 $\times $ curved surface area of hemisphere……….(1)
First we will find the CSA of the cylinder. The formula for finding the CSA of a cylinder $=2\pi rh$
Here, we will substitute r = 3.5 cm and h = 10 cm. Also, $\pi =\dfrac{22}{7}$, then we get,
$\begin{align}
& CSA\ of\ cylinder=2\times \dfrac{22}{7}\times 3.5\times 10c{{m}^{2}} \\
& =2\times \dfrac{22}{7}\times 35c{{m}^{2}} \\
& =2\times 22\times 5c{{m}^{2}} \\
& =22\times 10c{{m}^{2}} \\
& =220c{{m}^{2}}..............\left( 2 \right) \\
\end{align}$
Now, we will find the CSA of the hemisphere. We know that the formula for finding CSA of hemisphere \[=2\pi {{r}^{2}}\].
Here, we have r = 3.5 cm, so putting the value of radius in above formula, we get,
$\begin{align}
& The\ CSA\ of\ one\ hemisphere=2\times \dfrac{22}{7}\times {{\left( 3.5 \right)}^{2}}c{{m}^{2}} \\
& =2\times \dfrac{22}{7}\times 3.5\times 3.5c{{m}^{2}} \\
& =2\times 22\times 0.5\times 3.5c{{m}^{2}} \\
& =44\times 0.5\times 3.5c{{m}^{2}} \\
& =77c{{m}^{2}} \\
\end{align}$
So now, as you can see, we have 2 hemispheres. Therefore,
The CSA of 2 hemisphere $=2\times 77c{{m}^{2}}$
$=154c{{m}^{2}}..........\left( 3 \right)$
Using the equation (1), (2) and (3) we will get,
Total surface area of article = CSA of cylinder + 2 $\times $ CSA of hemisphere
$\begin{align}
& =220+154 \\
& =374c{{m}^{2}} \\
\end{align}$
Hence, total surface area of article $=374c{{m}^{2}}$.
Note: Students may make a mistake by removing the CSA of two hemispheres from the CSA of the cylinder instead of adding in it. They may get the answer as $220-154=66c{{m}^{2}}$. But as you can see here, the CSA of the cylinder only covers the surface area of the vertical portion of the cylinder. So, for finding the total surface area of the article, we have to add the CSA of two hemispheres in the CSA of the cylinder.
That is,
TSA of article = curved surface area of cylinder + 2 $\times $ curved surface area of hemisphere.
We will be using the below formulas.
The formula for the CSA of cylinder $=2\pi rh\ sq.unit$
The formula for the CSA of hemisphere $=2\pi {{r}^{2}}\ sq.unit$
Complete step-by-step answer:
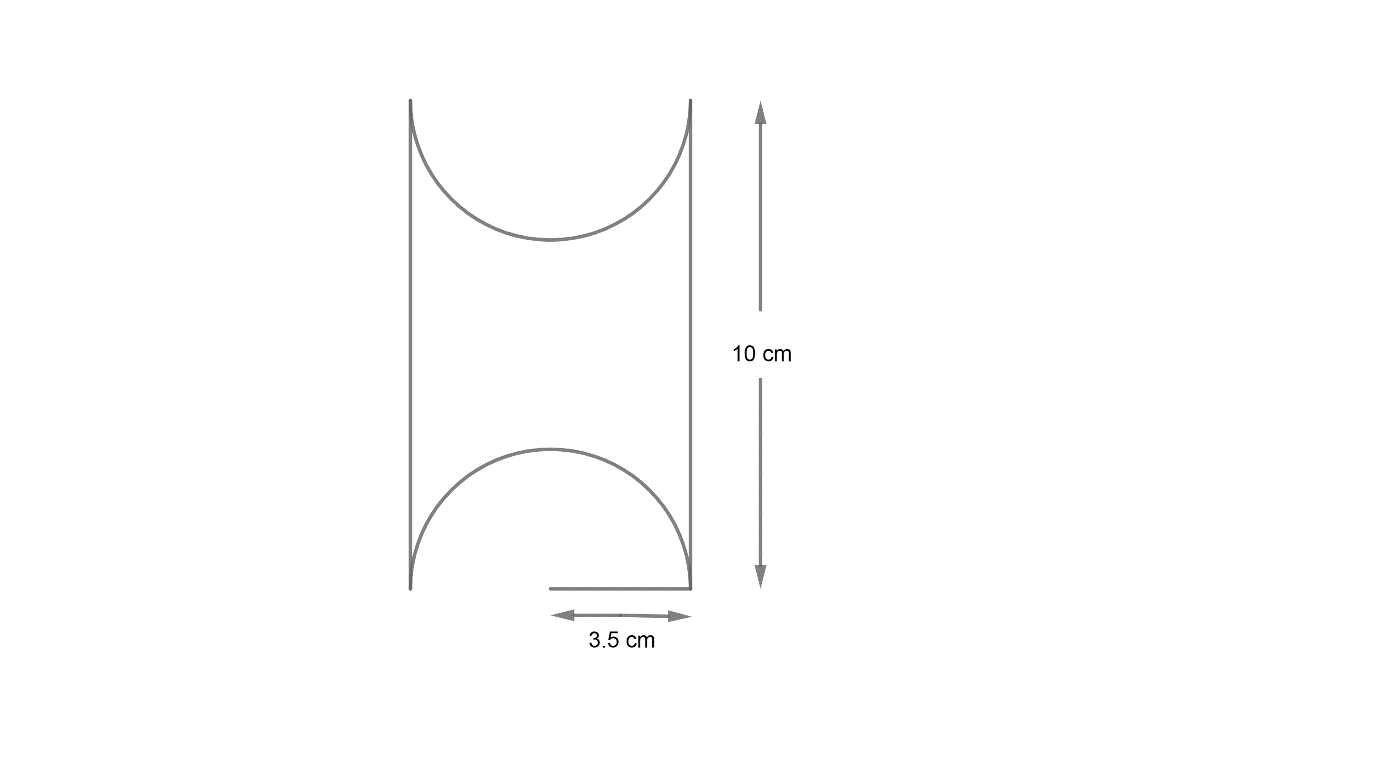
Let us consider the figure as shown,

Here, we have been given the height of the cylinder as h = 10cm and the radius of the cylinder is given as r = 3.5 cm.
Now, we can say that since the hemisphere is scooped out from the cylinder, the radius of the hemisphere will be the same as the radius of the cylinder.
Hence, we get the radius of the hemisphere = 3.5 cm.
Now, we have to compute the total surface area (TSA) of article = the curved surface area of cylinder + 2 $\times $ curved surface area of hemisphere……….(1)
First we will find the CSA of the cylinder. The formula for finding the CSA of a cylinder $=2\pi rh$
Here, we will substitute r = 3.5 cm and h = 10 cm. Also, $\pi =\dfrac{22}{7}$, then we get,
$\begin{align}
& CSA\ of\ cylinder=2\times \dfrac{22}{7}\times 3.5\times 10c{{m}^{2}} \\
& =2\times \dfrac{22}{7}\times 35c{{m}^{2}} \\
& =2\times 22\times 5c{{m}^{2}} \\
& =22\times 10c{{m}^{2}} \\
& =220c{{m}^{2}}..............\left( 2 \right) \\
\end{align}$
Now, we will find the CSA of the hemisphere. We know that the formula for finding CSA of hemisphere \[=2\pi {{r}^{2}}\].
Here, we have r = 3.5 cm, so putting the value of radius in above formula, we get,
$\begin{align}
& The\ CSA\ of\ one\ hemisphere=2\times \dfrac{22}{7}\times {{\left( 3.5 \right)}^{2}}c{{m}^{2}} \\
& =2\times \dfrac{22}{7}\times 3.5\times 3.5c{{m}^{2}} \\
& =2\times 22\times 0.5\times 3.5c{{m}^{2}} \\
& =44\times 0.5\times 3.5c{{m}^{2}} \\
& =77c{{m}^{2}} \\
\end{align}$
So now, as you can see, we have 2 hemispheres. Therefore,
The CSA of 2 hemisphere $=2\times 77c{{m}^{2}}$
$=154c{{m}^{2}}..........\left( 3 \right)$
Using the equation (1), (2) and (3) we will get,
Total surface area of article = CSA of cylinder + 2 $\times $ CSA of hemisphere
$\begin{align}
& =220+154 \\
& =374c{{m}^{2}} \\
\end{align}$
Hence, total surface area of article $=374c{{m}^{2}}$.
Note: Students may make a mistake by removing the CSA of two hemispheres from the CSA of the cylinder instead of adding in it. They may get the answer as $220-154=66c{{m}^{2}}$. But as you can see here, the CSA of the cylinder only covers the surface area of the vertical portion of the cylinder. So, for finding the total surface area of the article, we have to add the CSA of two hemispheres in the CSA of the cylinder.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

State and explain Ohms law class 10 physics CBSE

Distinguish between soap and detergent class 10 chemistry CBSE

a Why did Mendel choose pea plants for his experiments class 10 biology CBSE

What is a "free hit" awarded for in limited-overs cricket?

Draw the diagram of the sectional view of the human class 10 biology CBSE




