Question

A wire of length $l$ and mass $m$ is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is:

\[\begin{align}
  & A.\dfrac{Gml}{\pi l}\text{ along x-axis} \\
 & \text{B}\text{.}\dfrac{Gm}{\pi l}\text{ along the y-axis} \\
 & \text{C}\text{.}\dfrac{2\pi Gm}{{{l}^{2}}}\text{ along the y-axis} \\
 & \text{D}\text{.}\dfrac{2\pi Gm}{{{l}^{2}}}\text{ along the x-axis} \\
\end{align}\]

Answer 1

Hint: We know that the gravitational field is a vector which has two components. The perpendicular and the vertical component of the vector. Due to the symmetry of the semi-circle, we can say that one of the components gets cancelled.

Formula used:
\[E=\int\limits_{0}^{\pi }{dE\sin \theta }\]

Complete step-by-step answer:
We know that the gravitational field is a non-contact force. We know that gravitational force is given as $F=\dfrac{-GMm}{r^{2}}$, where $G$ is the gravitational constant, $M$ and $m$ is the mass of the bigger and the smaller objects which are at a distance $r$ with respect to each other.
Then the electric field is given as, $E=\dfrac{F}{M}$
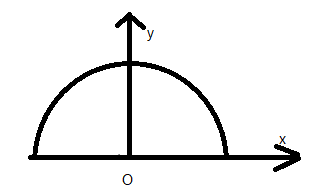
Consider a bent wire of length $l$and mass $m$, let us assume that the radius of the semicircle be $R$. Consider the gravitational field intensity at the centre of the semicircle O. Due to the symmetry of the semicircle clearly the x component of the cancels each other. Thus the total gravity field is along the y-axis only.
Let us assume that $l=\pi R$.
We know that the gravitational field, since the mass is distributed continuously on the ring, it is given as \[E=\int\limits_{0}^{\pi }{dE\sin \theta }\]
\[\begin{align}
  & \Rightarrow \int\limits_{0}^{\pi }{\dfrac{G.dM}{{{R}^{2}}}\sin \theta } \\
 & \Rightarrow \int\limits_{0}^{\pi }{\dfrac{G.\left( \dfrac{M}{\pi }d\theta \right)}{{{R}^{2}}}\sin \theta } \\
 & \Rightarrow \dfrac{2GM}{\pi {{R}^{2}}} \\
 & \Rightarrow \dfrac{2GM\pi }{{{l}^{2}}} \\
\end{align}\]
Hence the answer is \[\text{C}\text{.}\dfrac{2\pi Gm}{{{l}^{2}}}\text{ along the y-axis}\]

So, the correct answer is “Option C”.

Note: To find the total gravitational field, here we are integrating the electric field over the region. Since we are considering the semi-circle, we are integrating over the range $0$ to $\pi$. Also the angle for the integration varies here. Also note that, $m$ is the mass of the small object which is attracted to a bigger object of mass $M$. Since the $M >> m$, we are considering the effect of the small body for finding the field.