Question

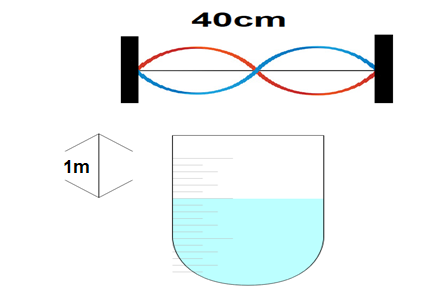
A wire of length 40 cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its fundamental mode as shown in figure. Assuming the speed of sound in air as 340 m/s, then the tension in the wire is $1156\times {{10}^{-X}}N$. Find the value of X.
   

Answer 1

Hint: The lowest resonant frequency of a vibrating object is called its fundamental frequency. The multiples of this frequency is known as 2nd harmonic frequency, 3rd harmonic frequency etc. the 2nd harmonic frequency will be twice of the fundamental harmonic frequency.

Complete answer:
In the question we have been given with some quantities,
Length of wire: 40cm or 0.4 meters
Mass of wire: 4g or $4\times {{10}^{-3}}$kg
Speed of Sound in Air: 340m/s
The Frequency of second harmonic of wire having Length (L) is given by,
$f=\dfrac{1}{L}\sqrt{\dfrac{T}{\mu }}$ ………… equation 1
Where T is the tension in the wire.
And $\mu $is mass per unit length which is given by $\mu =\dfrac{m}{L}$
$\mu =\dfrac{4\times {{10}^{-3}}}{0.4}$
$\mu =0.01kg/m$
Put the value of $\mu $in the above formula for second harmonic of wire
$f=\dfrac{1}{0.4}\sqrt{\dfrac{T}{0.01}}$
Now, Fundamental mode of vibration for the air column is given by,
${{f}_{0}}=\dfrac{V}{4L}$
Where ${{f}_{0}}$ is the fundamental frequency for air column and V is the velocity of sound in air, and L=1m (depth)
${{f}_{0}}=\dfrac{340}{4\times 1}$
${{f}_{0}}$= 85Hz
Now put the value of ${{f}_{0}}$ in place of $f$ in equation 1
$85=\dfrac{1}{0.4}\sqrt{\dfrac{T}{0.01}}$
We get $T=11.56$N
Or we can write $T=1156\times {{10}^{-2}}N$
We have been given in question that the tension of wire is $1156\times {{10}^{-X}}N$
Now compare this with our value of T which we get in solution,
We get X=2
Hence this is our required solution

Note:
In the fundamental frequency for the air column, we have taken L as 1 meter and not as the length to wire because we are given that the water is 1 meter below the top of the tube. Please always remember to take the length according to the quantity we are finding, if you are finding the frequency of wire then you should take the length of wire.