Question

A wire is in the shape of a rectangle. Its length is 40cm and breadth is 22cm. If the same wire is re-bent in the shape of a square, what will be the measure of each side? Also find which shape encloses more area?

Answer 1

Hint: In the given question we have given a wire and two shapes, first rectangle and second square is made from it by bending. The total length or the perimeter of the wire is not changing. So, let’s find the perimeter of the rectangle first and then equate it to the area of the square to find the side of the square. Then by using the side, let’s find the area of the square.

Complete step-by-step answer:

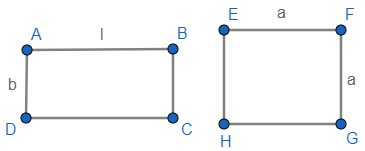
Firstly, the wire is in rectangular shape, so we will find the total length of the wire by calculating the perimeter of the rectangle. In a rectangle we have two lengths (l) and two breadths (b), so the total length or perimeter of the rectangle will be the sum of all the breadths and lengths.

Therefore, the formula for perimeter (P) of the rectangle is given by,
$\begin{align}
  & P=l+b+l+b \\
 & P=2(l+b).................(i) \\
\end{align}$

In the given question we have given,
Length, l = 40cm………….(p)
And, breadth, b = 22cm…………(q)

Substituting the values in equation (i), we get,
$P=2(40+22)$

Applying the BODMAS rule, we need to do addition within the brackets and then multiply,
$\begin{align}
  & \Rightarrow P=2\times 62 \\
 & \Rightarrow P=124cm \\
\end{align}$

This means the total length of the wire is 124cm. Now this wire is re-bent into a square that means the total length or perimeter of the square is equal to the total length of the wire. But we know that a square has four equal sides. If ‘a’ is the length of one side of the square then the perimeter of the square will be,
$P=a+a+a+a=4a$

As we know the total length of wire is 124cm which is equal to the perimeter of the square, therefore we can write,
$\begin{align}
  & 124=4a \\
 & \Rightarrow a=\dfrac{124}{4} \\
 & \Rightarrow a=31cm.........(r) \\
\end{align}$

It means the length of one side of the square is 31cm.

Now, we need to compare the areas of both figures, so we will calculate areas of both rectangle and the square,
The area of rectangle is given by the formula,
$A=l\times b$

Substituting the values from equation (p) and (q), we get,
$\begin{align}
  & A=40\times 22 \\
 & A=880c{{m}^{2}}...........(ii) \\
\end{align}$

Now the area of Square is given by formula,
$A=a\times a$

Substituting the values from equation (r), we get,
$\begin{align}
  & A=31\times 31 \\
 & A=961c{{m}^{2}}..............(iii) \\
\end{align}$

Comparing the values of the areas calculated from equation (ii) and (iii) we can say the area of the square is more than of the rectangle.

Hence, the square encloses more area than the rectangle made by re-bending the same wire.

Note: The caution must be taken when writing the formula for the perimeter $2\left( l+b \right)$ of the rectangle. It must not be confused with the area of the rectangle $\left( l\times b \right)$ because both look something similar.