Question

A wire in the shape of an equilateral triangle encloses an area $S\text{ c}{{\text{m}}^{2}}$. If the same wire is bent to form a circle then the area of the circle will be
(a) $\dfrac{\pi {{S}^{2}}}{\pi }$
(b) $\dfrac{3{{S}^{2}}}{\pi }$
(c) $\dfrac{3S}{\pi }$
(d) $\dfrac{3S\sqrt{3}}{\pi }$

Answer 1

Hint:We are using the same wire to form two different shapes. Therefore, the perimeters of these two shapes will be equal. We will formulate an equation using this information to establish a relation between the circle and the equilateral triangle. We will use the formula of the area of a triangle to find the side of the equilateral triangle in terms of the area $S\text{ c}{{\text{m}}^{2}}$. Then we will use the formula for the area of the circle to get the required answer.

Complete step by step answer:
Let us draw an equilateral triangle with side $a\text{ cm}$.

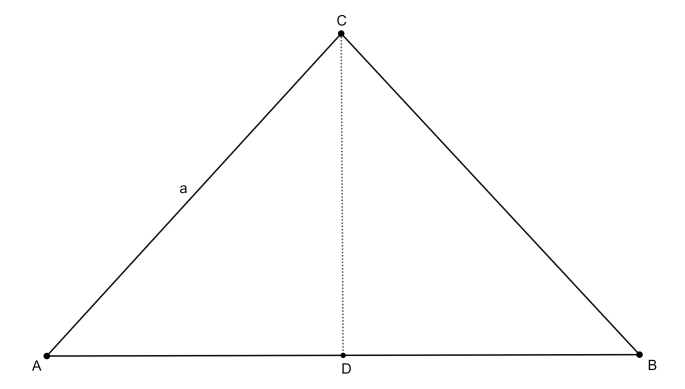
The perimeter of this triangle is ${{P}_{triangle}}=3a$. We know that the area of this equilateral triangle is $S\text{ c}{{\text{m}}^{2}}$. The formula for area of triangle is given by,
${{A}_{triangle}}=\dfrac{1}{2}\times b\times h$
where $b$ is the base of the triangle and $h$ is the height of the triangle. For this equilateral triangle, we have to calculate the height using Pythagoras theorem. We can use this theorem since $\Delta ADC$ is a right angled triangle. Therefore, we get
$\begin{align}
  & {{a}^{2}}={{\left( \dfrac{a}{2} \right)}^{2}}+{{h}^{2}} \\
 & \therefore {{h}^{2}}={{a}^{2}}-\dfrac{{{a}^{2}}}{4}=\dfrac{3{{a}^{2}}}{4} \\
 & \therefore h=\dfrac{\sqrt{3}a}{2} \\
\end{align}$
Now, we will substitute $b=a$ and $h=\dfrac{\sqrt{3}a}{2}$ in the above formula, in the following manner,
$S=\dfrac{1}{2}\times a\times \dfrac{\sqrt{3}a}{2}=\dfrac{\sqrt{3}{{a}^{2}}}{4}$.
Therefore, we have ${{a}^{2}}=\dfrac{4S}{\sqrt{3}}$.
As we are using the same wire to form the circle, the perimeter of the triangle and the perimeter of the circle is equal. The perimeter of circle with radius $r$ is given by ${{P}_{circle}}=2\pi r$.
Therefore, we have ${{P}_{circle}}={{P}_{triangle}}$. Substituting the values in this equation, we get
$\begin{align}
  & 2\pi r=3a \\
 & \therefore r=\dfrac{3a}{2\pi } \\
\end{align}$
Now, we will use the formula for area of circle. The area of circle is given by
${{A}_{circle}}=\pi {{r}^{2}}$
Substituting the value of $r$ in the above formula, we get
$\begin{align}
  & {{A}_{circle}}=\pi \times {{\left( \dfrac{3a}{2\pi } \right)}^{2}} \\
 & =\pi \times \dfrac{9{{a}^{2}}}{4{{\pi }^{2}}}
\end{align}$
Substituting the value of ${{a}^{2}}=\dfrac{4S}{\sqrt{3}}$, we get
$\begin{align}
  & {{A}_{circle}}=\pi \times \dfrac{9}{4{{\pi }^{2}}}\times \dfrac{4S}{\sqrt{3}} \\
 & =\dfrac{3S\sqrt{3}}{\pi }
\end{align}$
Hence, the correct option is (d).
Note:
In this question, the important part is realizing the relations between perimeters and areas of two different objects. We need to make correct substitutions for the radius of the circle and the side of the equilateral triangle. There is a possibility of messing up the calculations while substituting the values of variables in terms of other variables. To avoid this, it is useful to use different labels and write the formulae explicitly.