Question

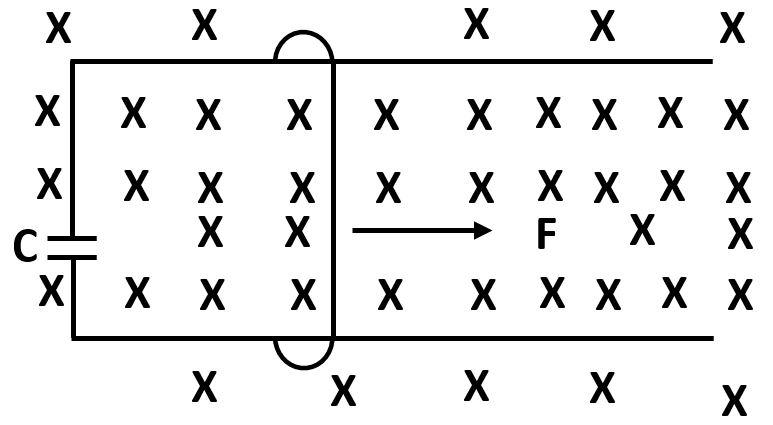
A wire having mass $m$ and length $l$ can freely slide on a pair of parallel smooth horizontal rails placed in a vertical magnetic field $B$. The rails are connected by a capacitor of capacitance $C$. The electric resistance of the rails and the wire is zero. If a constant force $F$ acts on the wire as shown in the figure. Then, the acceleration of the wire can be given as?

A. $a = \dfrac{{{C^2}{B^2}l - F}}{m}$
B. $a = \dfrac{F}{{m + CBl}}$
C. $a = \dfrac{{F{C^2}{B^2}l}}{m}$
D. $a = \dfrac{F}{{m + C{B^2}{l^2}}}$

Answer 1

Hint: Find a relation between charge and magnetic field using the relation of potential and charge. Then differentiate the charge to find current. Then use the formula of force in terms of acceleration as well as in terms of magnetic field. Compare them to solve this question.

Complete step by step answer:
Let the velocity of the wire be $v$
And the charge on the capacitor be $q$
It is given that the length of the wire is $l$
Mass of the wire is $m$
The wire is placed in the magnetic field $B$
Then emf induced in the wire can be given by
$e = Blv$
The potential difference across the terminals of a capacitor and the emf induced in the wire must be equal as they are connected in parallel.
$ \Rightarrow V = e$
We know that,
$q = CV$
$ \Rightarrow V = \dfrac{q}{C}$
Therefore, we get
$\dfrac{q}{C} = Blv$
$ \Rightarrow q = BClv$
Differentiating it with respect to $t$ we get
$i = \dfrac{{dq}}{{dt}}$
$ \Rightarrow i = \dfrac{d}{{dt}}\left( {CBlv} \right)$
Since, $CBl$ is constant, we get
$ \Rightarrow i = CBl\dfrac{d}{{dt}}\left( v \right)$
Since, $\dfrac{{dv}}{{dt}} = a$
We get
$i = CBla$
Where,
$a$ is acceleration of the wire
Now, the net force on the rod will be the force due to gravity and the force due to the magnetic field.
${F_{net}} = {F_g} - {F_m}$ . . . (1)
Where,
${F_g} = mg$ is the force due to gravity
${F_m} = ilB$ is the force due to the magnetic field.
And ${F_{net}} = ma$ is the resultant force
$ \Rightarrow ma = mg - ilB$
Substituting the value of $i$ in the above equation, we get
$ma = mg - CBlaBl$
By rearranging it we get
$(m + C{B^2}{l^2})a = mg$
$ \Rightarrow a = \dfrac{F}{{m + C{B^2}{l^2}}}$
Therefore, from the above explanation, the correct answer is, option (D) $a = \dfrac{F}{{m + C{B^2}{l^2}}}$

Note:Net resultant force is actually the sum of all the forcing acting on the body. And still we have done subtraction in equation (1) because, force is a vector quantity and the net resultant force is the vector sum of all the forces. And since, the force due to gravity and the force due to magnetic field will be acting in the opposite direction, we will subtract them.