Question

A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.\[\]

Answer 1

Hint: The maximum light may only come through maximum area. We take the length of the rectangle as $x$ and breadth as $y$. We use the value of the given semi-perimeter to express $y=f\left( x \right)$. We put $y$ in the expression for the total area of the window and maximize it to find $x$ as a critical point using the second derivative test. We then find $y.$\[\]

Complete step-by-step solution
We know from the second derivative test that the function $f\left( x \right)$ will have a local maxima at critical point $x=c$ if ${{f}^{''}}\left( c \right)<0$. The critical points are the solutions of ${{f}^{'}}\left( x \right)=0$.\[\]

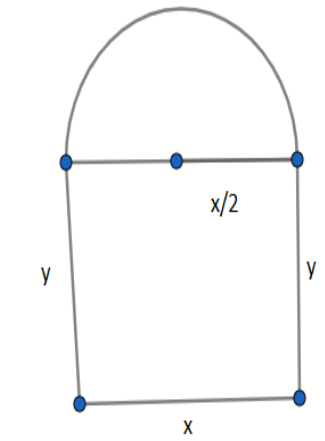
We are given that a window is in the form of a rectangle surmounted by a semicircular opening. If we want maximum light to pass through the opening we want the light passed through the entire area made by a rectangular window and the semi-circular opening. \[\]
Let us assume that the length of the rectangle is $x$ and breadth is $y$. So the radius of the semi-circular opening is $\dfrac{x}{2}.$ It is given in the question that the perimeter of the entire window is 10m. We have
\[\begin{align}
  & 2\left( x+y \right)+\pi \left( \dfrac{x}{2} \right)-x=10 \\
 & \Rightarrow x+2y+\dfrac{\pi x}{2}=10 \\
 & \Rightarrow y=5-x\left( \dfrac{1}{2}+\dfrac{\pi }{4} \right)...(1) \\
\end{align}\]
The total area of the window is the sum of the areas of rectangle and semi-circle. We have,
\[A=xy+\dfrac{1}{2}\pi {{\left( \dfrac{x}{2} \right)}^{2}}\]
We put the obtained values of $y$ in the above equation to get,
\[\begin{align}
  & A=x\left( 5-x\left( \dfrac{1}{2}+\dfrac{\pi }{4} \right) \right)+\dfrac{1}{2}\pi {{\left( \dfrac{x}{2} \right)}^{2}} \\
 & \Rightarrow A=5x-\dfrac{1}{2}{{x}^{2}}-\dfrac{\pi }{4}{{x}^{2}}+\dfrac{\pi }{8}{{x}^{2}} \\
 & \Rightarrow A=5x-\dfrac{1}{2}{{x}^{2}}-\dfrac{\pi }{8}{{x}^{2}} \\
\end{align}\]
We have to maximize the area. Let us differentiate $A$ once with respect to $x$ and the equate to 0 so that we can find critical points where $A$ can have a maxima. We have,
\[\begin{align}
  & \dfrac{dA}{dx}=5-x-\dfrac{\pi x}{4}=0 \\
 & \Rightarrow x=\dfrac{5}{1+\dfrac{\pi }{4}}=\dfrac{20}{\pi +4} \\
\end{align}\]
We have obtained only one critical point $x=\dfrac{20}{\pi +4}$. We find the value of the second derivative of $A$ at $x=\dfrac{20}{\pi +4}$.
\[\begin{align}
  & \dfrac{{{d}^{2}}A}{dx}=\dfrac{d}{dx}\left( \dfrac{dA}{dx} \right) \\
& \Rightarrow \dfrac{{{d}^{2}}A}{dx}=\dfrac{d}{dx}\left( 5-x-\dfrac{\pi x}{4} \right)=-1-\dfrac{\pi }{4} \\
\end{align}\]
We see that $\dfrac{{{d}^{2}}A}{dx}<0$ for all $x\in R$ including $x=\dfrac{20}{\pi +4}$. So $A$ will have a maxima at $x=\dfrac{20}{\pi +4}$. We put $x$ in equation (1) and get,
\[\begin{align}
  & y=5-\left( \dfrac{20}{\pi +4} \right)\left( \dfrac{1}{2}+\dfrac{\pi }{4} \right)=5-\left( \dfrac{20}{\pi +4} \right)\left( \dfrac{2+\pi }{4} \right) \\
 & =5-5\dfrac{\pi +2}{\pi +4}=5\left( \dfrac{\pi +2-\pi -4}{\pi +4} \right)=5\dfrac{2}{\pi +4}=\dfrac{10}{\pi +4} \\
\end{align}\]
So the dimension of the window to admit maximum light through the whole opening is length $\dfrac{20}{\pi +4}$m and breadth $\dfrac{10}{\pi +4}$m.\[\]

Note: We need to be careful that the perimeter of the window does not include the diameter of the semicircle. We note that if the second derivative would have ${{f}^{''}}\left( c \right)=0$ we would have done a third derivative test and so on. The function $f\left( x \right)$ has a maxima at $x=c$ if ${{f}^{n+1}}\left( c \right) < 0$ and ${{f}^{'}}\left( c \right)={{f}^{''}}\left( c \right)=...={{f}^{n}}\left( c \right)=0$