Question

A whistle emitting a loud sound of frequency 540Hz is whirled in a horizontal circle of radius 2m and at a constant angular speed of $15\ rad.{{s}^{-1}}$. The speed of sound is \[330\ m.{{s}^{-1}}\]. The ratio of highest to the lowest frequency heard by the listener standing at a large distance from the center of the circle is?
A. 1.0
B. 1.1
C. 1.2
D. 1.4

Answer 1

Hint: The concept of Doppler effect is required to solve this problem. The Doppler’s formula required to solve this problem is, \[f={{f}_{0}}[\dfrac{{{c}_{s}}+{{v}_{l}}}{{{c}_{s}}+{{v}_{s}}}]\], where ${{v}_{s}}$is the velocity of the source and \[{{v}_{l}}\]is the velocity of the receiver. ${{f}_{0}}$ is the frequency of the whistle originally.

Complete step-by-step answer:
Let’s understand the Doppler’s formula: \[f={{f}_{0}}[\dfrac{{{c}_{s}}+{{v}_{l}}}{{{c}_{s}}+{{v}_{s}}}]\].
 Here the values of the velocity of the listener and that of the source is both positive and negative depending upon the direction of the movement of the source and the listener. Hence, if the listener is moving towards the source, then the value of \[{{v}_{l}}\] will be positive. If the listener is static or not moving, then the value of \[{{v}_{l}}\] would be zero and lastly, when the receiver is moving away from the source, then the value of \[{{v}_{l}}\] will be negative.
Similarly, if the source is moving away from the listener, then the value of ${{v}_{s}}$ will be positive. If the source is static or not moving, then the value of ${{v}_{s}}$ would be zero and lastly, when the source is moving towards the listener, then the value of ${{v}_{s}}$ will be negative.
Now, let’s make a diagram of the problem.

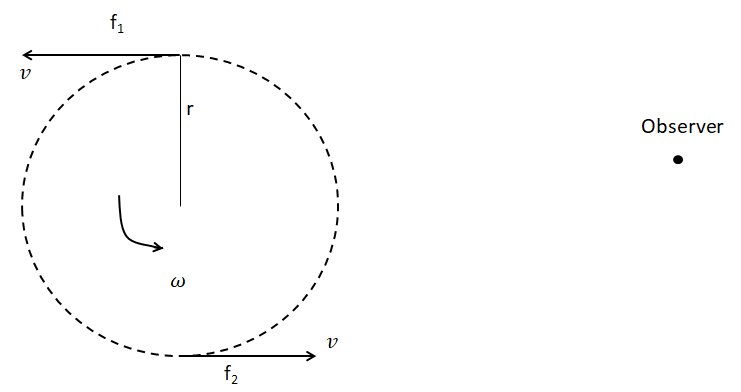
As per the problem, ${{f}_{0}}=540Hz$, is the frequency of the whistle originally.
The velocity of sound in air is given to be, \[{{c}_{s}}=330\,m{{s}^{-1}}\].
The angular velocity of the whistle is given to be: $\omega =15\ rad.{{s}^{-1}}$.
The radius of the circular motion followed by the whistle in the horizontal plane is: r=2m.
Therefore, the tangential velocity of the whistle will be: $v=\omega r$.
Therefore, $v=\omega r\Rightarrow v=15\times 2=30m.{{s}^{-1}}$.
When the whistle is moving towards the listener, the frequency of the whistle as heard by the listener is ${{f}_{2}}$given by: \[{{f}_{2}}={{f}_{0}}[\dfrac{{{c}_{s}}}{{{c}_{s}}-{{v}_{s}}}]\Rightarrow {{f}_{2}}=540[\dfrac{330}{330-30}]\Rightarrow {{f}_{2}}=540[\dfrac{330}{300}]Hz\].
Hence, the highest frequency of the whistle is: \[{{f}_{2}}=540[\dfrac{330}{300}]Hz\].
Similarly, when the whistle is moving away from the listener, the frequency of the whistle as heard by the listener is${{f}_{1}}$given by: \[{{f}_{1}}={{f}_{0}}[\dfrac{{{c}_{s}}}{{{c}_{s}}+{{v}_{s}}}]\Rightarrow {{f}_{1}}=540[\dfrac{330}{330+30}]\Rightarrow {{f}_{1}}=540[\dfrac{330}{360}]Hz.\]
Hence, the lowest frequency of the whistle is: \[{{f}_{1}}=540[\dfrac{330}{360}]Hz\].
We are asked to find the ratio of the highest to the lowest emitted frequency as heard by the listener. Hence, the ratio is: $\dfrac{{{f}_{2}}}{{{f}_{1}}}=\dfrac{540[\dfrac{330}{300}]}{540[\dfrac{330}{360}]}\Rightarrow \dfrac{{{f}_{2}}}{{{f}_{1}}}=\dfrac{360}{300}=1.2$.
Therefore, the solution is 1.2, which is Option C.

Note: From the solution, we can observe that the highest frequency of the whistle is when the whistle is travelling towards the listener. Hence, in the general scenario, when a source emitting sound travels towards a stationary listener, the listener hears the frequency of the sound to be higher than the original frequency of the sound emitted by the source.
Similarly, when the source is travelling away from the listener and emitting a sound, then the stationary listener finds the sound heard by him to be of a lesser frequency than the originally emitted sound by the source.