Question

A wheelchair ramp that is 13.5 feet long has a 15 degrees angle of depression. How high off the ground is the ramp?

Answer 1

Hint: In the given problem, the angle of depression is the angle that the top of the ramp makes with the horizontal. Now, this angle of depression is also equal to the angle of elevation of the ramp from the ground. Also, the slant length of the ramp is known to us. So, the projection of this slant length on the vertical and horizontal axes will give us the length of ramp along the surface of the ground and its height above the ground.

Complete answer:
Let us try to understand the problem with the given figure:

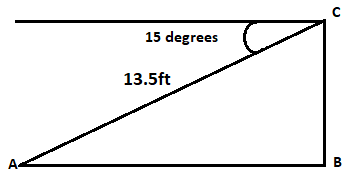
In the above diagram the angle that is making ${{15}^{0}}$ with the horizontal is the angle of depression. Its conjugate angle is the angle at which the ramp is with the ground. This angle is the angle of elevation and its value is also ${{15}^{0}}$ .
Now, to find the height of the ramp (say h), we need to find the vertical projection of the ramp’s slant height.
Therefore, in $\vartriangle ABC$ , we can write as:
$\Rightarrow \sin {{15}^{0}}=\dfrac{BC}{AC}$
Where,
BC is the height of the ramp $=h$
AC is the slanted length of the ramp $=13.5ft$
Putting these values in the above equation, we get:
$\begin{align}
  & \Rightarrow \sin {{15}^{0}}=\dfrac{h}{13.5} \\
 & \Rightarrow h=\sin {{15}^{0}}\times 13.5ft \\
 & \\
\end{align}$
Using the value of, $\sin {{15}^{0}}=\left( \dfrac{\sqrt{3}-1}{2\sqrt{2}} \right)$
We get:
$\begin{align}
  & \Rightarrow h=\left( \dfrac{\sqrt{3}-1}{2\sqrt{2}} \right)\times 13.5ft \\
 & \Rightarrow h=0.26\times 13.5ft \\
 & \Rightarrow h=3.51ft \\
\end{align}$
Hence, the height of the ramp comes out to be $3.51ft$ .

Note:
The meaning of basic terms like Angle of elevation and Angle of Depression should be well known to us. Also $(\sin 15,\cos 15,\tan 15)$and $(\sin 75,\cos 75,\tan 75)$ are some non-trivial trigonometric terms but their values should be known to us. But, in case one can’t remember these, then we can always use the formulas of $\sin (A+B),\sin (A-B),\cos (A+B),\tan (A-B)$etc. to find their values quickly .