Question

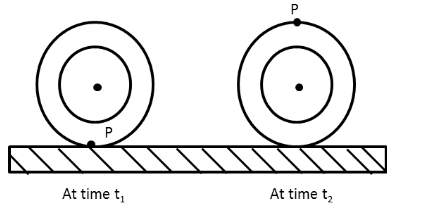
A wheel with radius \[45\,{\text{cm}}\] rolls without slipping along a horizontal floor as shown in figure. P is a dot pointed on the rim of the wheel. At time \[{t_1}\], P is at the point of contact between the wheel and the floor. At a later time \[{t_2}\], the wheel has rolled, through one-half of a revolution. What is the displacement of P during this interval?

A. \[90\,{\text{cm}}\]
B. \[168\,{\text{cm}}\]
C. \[40\,{\text{cm}}\]
D. Data insufficient

Answer 1

Hint: Calculate the horizontal and vertical displacements of point P. Then calculate the resultant displacement of the point P.

Formulae used:
The circumference \[C\] of the circle is given by
\[ \Rightarrow C = 2\pi r\] …… (1)
Here, \[r\] is the radius of the circle.
The resultant displacement \[s\] is given by
\[ \Rightarrow s = \sqrt {s_x^2 + s_y^2} \] …… (2)
Here, \[{s_x}\] is the horizontal component of displacement and \[{s_y}\] is the vertical component of displacement.

Complete step by step answer:
Calculate the horizontal displacement of the point P between the times \[{t_1}\] to \[{t_2}\].
The horizontal displacement \[{s_x}\] of the point P is equal to half of the circumference \[C\] of the wheel.
\[ \Rightarrow {s_x} = \dfrac{C}{2}\]
Substitute \[2\pi r\] for \[C\] in the above equation.
\[ \Rightarrow {s_x} = \dfrac{{2\pi r}}{2}\]
Substitute \[3.14\] for \[\pi \] and \[45\,{\text{cm}}\] for \[r\] in the above equation.
\[{s_x} = \dfrac{{2\left( {3.14} \right)\left( {45\,{\text{cm}}} \right)}}{2}\]
\[ \Rightarrow {s_x} = 141.3\,{\text{cm}}\]
Hence, the horizontal displacement of the point P is \[141.3\,{\text{cm}}\].
Calculate the vertical displacement of the point P between the times \[{t_1}\] to \[{t_2}\].
The vertical displacement \[{s_y}\] of the point P is equal to the diameter of the wheel which is twice the radius \[r\] of the wheel.
\[ \Rightarrow {s_y} = 2r\]
Substitute \[45\,{\text{cm}}\] for \[r\] in the above equation.
\[ \Rightarrow {s_y} = 2\left( {45\,{\text{cm}}} \right)\]
\[ \Rightarrow {s_y} = 90\,{\text{cm}}\]
Hence, the vertical displacement of the point P is \[90\,{\text{cm}}\].
Now calculate the resultant displacement \[s\] of the point P.
Substitute \[141.3\,{\text{cm}}\] for \[{s_x}\] and \[90\,{\text{cm}}\] for \[{s_y}\] in equation (2).
\[ \Rightarrow s = \sqrt {{{\left( {141.3\,{\text{cm}}} \right)}^2} + {{\left( {90\,{\text{cm}}} \right)}^2}} \]
\[ \Rightarrow s = 167.5\,{\text{cm}}\]
\[ \Rightarrow s = 168\,{\text{cm}}\]
Therefore, the displacement of the point P is \[168\,{\text{cm}}\].
Hence, the correct option is B.

Note:One may directly determine the diameter of the wheel to calculate the displacement of point P. But it is the vertical displacement and not the resultant displacement.