Question

A wheel of radius R is free to rotate about its natural axis and I is its moment of inertia. If a tangential force F is applied on the wheel along its rim, then the angular acceleration of wheel is:
A. $IFR$
B. $\dfrac{{FR}}{I}$
C. $\dfrac{{IF}}{R}$
D. $\dfrac{{IR}}{F}$

Answer 1

Hint: Initially the wheel is free to rotate about its natural axis, therefore no angular acceleration is observed. But, with the application of tangential force F, torque is observed. This torque gives rise to angular acceleration. So, first, we need to determine the torque due to the force. This can be used to find the angular acceleration of the wheel.
Formula used:
$\tau = FR\sin \theta $
$\tau = I\alpha $

Complete answer:
It is given in the question that the wheel of radius R is free to rotate about its natural axis, with the moment of Inertia I. And it is acted upon by a force F along its rim, as drawn in the figure.

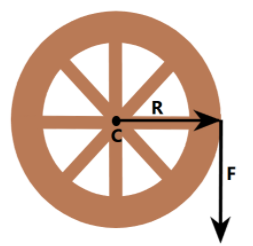
Here, the force F is acting as torque along R. Torque is the tendency of the force applied at distance, causing rotation.
The torque due to the given force F is given by,
$\eqalign{
  & \vec \tau = \vec F \times \vec R \cr
  & \Rightarrow \tau = FR\sin \theta \cr} $
 Here, the ‘$ \times $’ indicates the cross product of the vectors and ‘$\theta $’ is said to be in the angle between the force and the radius.
From the diagram drawn above, we can see that $\theta = {90^ \circ }$. So, the torque, in this case, will be
$\tau = FR\sin {90^ \circ } = FR$
The torque can also be written as $\tau = I\alpha $. This denotes that due to the torque, on the wheel whose moment of Inertia is given as ‘$I$’, an angular acceleration ‘$\alpha $’ acts on the wheel.
So, we can write
$\eqalign{
  & \tau = I\alpha = FR \cr
  & \Rightarrow \alpha = \dfrac{{FR}}{I} \cr} $

Therefore, the correct option is B.

Note:
Torque in rotational form is analogous to force in the linear form.
The above question can also be solved in the term of dimensional analysis. The angular acceleration has dimensions of $[{M^0} {L^0} {T^{-2}}]$, as its unit is ${rad/{s^2}}$ but radians do not have dimensions. Therefore, the option which has the same dimension will be the answer.
One might ask why there is no angular acceleration while the wheel is rotating about its axis. As there is no external force acting upon the wheel, initially, the wheel must be under constant angular velocity. As the angular velocity is constant the angular acceleration is zero, initially.