Question

A wheel makes 360 revolutions in a minute. Through how many radians does it turn in one second?

Answer 1

Hint: A wheel makes 360 revolutions in a minute and we know that one minute contains 60 seconds so in 60 seconds a wheel makes 360 revolutions. By unitary method we can find in 1 second how many revolutions a wheel has made which can be done by dividing 360 by 60. Now, we have to write answers in radians so $ {{360}^{\circ }} $ is equal to $ 2\pi $ radians. And one revolution sweeps $ 2\pi $ radians so multiply $ 2\pi $ with the number of revolutions we have found above to get an answer in radians.

Complete step-by-step answer:
It is given that a wheel makes 360 revolutions in a minute.
We know that one minute is comprised of 60 seconds so rewriting the above language we get,
In 60 seconds, a wheel makes 360 revolutions so by unitary method in 1 second the revolutions made by a wheel are the division of 360 by 60 which is equal to:
 $ \dfrac{360}{60}=6 $
Hence, a wheel makes 6 revolutions in 1 second.
Now, we know that the angle swept by the wheel in 1 revolution is $ {{360}^{\circ }} $ or $ {{360}^{\circ }} $ is also equal to $ 2\pi $ radians.
As we have to find the radians in 6 revolutions so we are multiplying 6 by $ 2\pi $ we get,
 $ 12\pi $ radians
Hence, a wheel turns $ 12\pi $ radians in 1 second.

Note: In the below, we are going to show how 1 revolution is equal to $ {{360}^{0}} $ . We are assuming a wheel by a circle with centre O. And let us assume a point B on the circle.
After one revolution of the circle the point B comes to its initial point after traversing through a complete circle.
 

After making one revolution by the circle, the point B coincides with its original position. The point B has traversed through a complete circle in 1 revolution. We know that a complete circle makes $ {{360}^{\circ }} $ at the centre. In the below diagram, we have shown a circle with $ {{360}^{\circ }} $ at the centre.
 

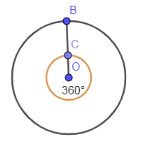
From the above figure, you can see that in 1 revolution, point B has traversed $ {{360}^{\circ }} $ angle at the centre.