Question

(a) What would you conclude from the velocity-time graph of the cyclist from the given graph?
(b) Velocity changes linearly if acceleration ____.

Answer 1

Hint: Acceleration of a body is defined as the time rate of change of velocity of the body. If the acceleration changes linearly with time, velocity changes non-linearly with time. If the acceleration is uniform (constant), velocity changes linearly with time.

Complete step by step answer:
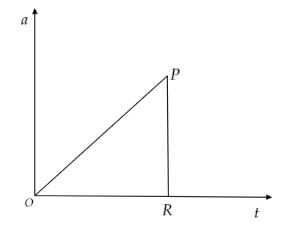
(a) We know that the formula for acceleration $\vec a = \dfrac{{d\vec v}}{{dt}}$, where $\vec v$ is the velocity. From the given acceleration-time graph, acceleration $a$ changes linearly with time $t$ from O to P. For better understanding let’s do the mathematics. From O to P, acceleration $a \propto t$.
$ \Rightarrow a = Ct$
Where $C$ is a constant.

Now $\dfrac{{dv}}{{dt}} = Ct$
$ \Rightarrow dv = Ctdt$
Integrate the above equation
$ \Rightarrow \int {dv} = \int {Ctdt} $
$ \Rightarrow v = C\dfrac{{{t^2}}}{2} + {C_1}$
Where ${C_1}$ is a constant of integration.
For simplicity let ${C_1} = 0$ and $\dfrac{C}{2} = K$
$ \Rightarrow v = K{t^2}$

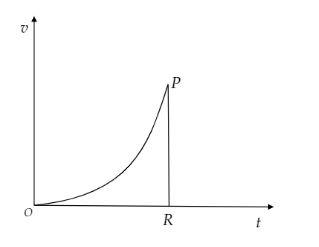
From O to P, the velocity-time graph is a curve. i.e., when acceleration varies linearly with time, velocity varies non-linearly with time. After the point P, the acceleration becomes zero suddenly to the point R. So, velocity is either zero or constant. Since the given graph is not extended after the point R, let velocity is zero. The velocity-time graph for the given graph is drawn below.

(b) Now it is given that velocity changes linearly with time.It is required to find the variation of acceleration with time.Again, we will do mathematics for better understanding.Since velocity $v$ varies linearly with time $t$, $v \propto t$.
$ \Rightarrow v = Ct$
Where $C$ is a constant.
Now acceleration $a = \dfrac{{dv}}{{dt}}$
Substitute the value of velocity in the above formula.
$ \Rightarrow a = \dfrac{d}{{dt}}\left( {Ct} \right)$
$ \therefore a = C$
i.e., acceleration is constant.
Hence, velocity changes linearly with time if acceleration is constant or uniform.

Note: When acceleration is zero, there are two cases of the motion; (1) velocity is zero, (2) velocity is constant. But when velocity is zero, acceleration has only one value that is zero. These can be shown from the relation $a = \dfrac{{dv}}{{dt}}$.