Question

(a) What is the difference between ‘distance travelled’ by a body and its ‘displacement’? Explain with the help of a diagram.
(b) An ant travels a distance of $8\,cm$ from \[P\] to \[Q\] and then moves a distance of $6\,cm$ at right angles to \[PQ\]. Find its resultant displacement.

Answer 1

Hint: The displacement is said to be given by the change in position from one location to the other while the distance is concerned with the path that is taken. The Pythagoras theorem is applied in order to find out the resultant displacement of the ant. The distance and displacement quantities are distinguished with respect to their concepts.

Complete step by step answer:
The problem revolves around the concept of distance and displacement. In order to determine the difference between them we first need to know their concepts.

(a) Distance is defined as the length of the actual path travelled by an object in motion from one point to another. The point from which the body starts its motion is known as the initial position of the body and the point at which the body stops its motion or in other words the position where the body comes back again to the state of rest is known as the final position of the body.

The displacement is given by the difference between the initial and final points of the particle that is travelling regardless of the path. The displacement is independent of the path traversed by the particle. It only depends on the initial and the final values of the particle or in other words it is said to consider only the source and destination points. This proves to be the main differences between the distance and displacement quantities.

Let us now take an example to explain their difference more clearly. The below diagram illustrates a path from $A$ to $B$. Let us say that the original path travelled by an object is through the curve or the arc $AB$. This is said to be the total distance covered or travelled by the body. However, the displacement is given by the straight line path $AB$ since it takes the shortest route.

(b) A similar concept to that seen in the example taken in part a) is applied to part b) as well. The diagram below illustrates the path of the ant:

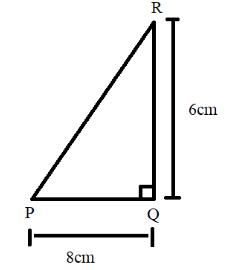
The original path in which the ant travels is given as the distance. This distance covered by the ant is said to be first from $P$ to $Q$ and then from $Q$ to $R$. This is the actual path of the ant which is said to be the distance over here given as $PQ + QR$.However, we are asked to find out the displacement of the path travelled by the ant.

The displacement is said to be concerned only with the initial and final values of the ant and is independent of the original path taken. Displacement always chooses the shortest path to cover the distance when there is more than one path to get to the destination location. Due to this reason the resultant displacement will be given by the path $PR$.

From the diagram above we can clearly see that it happens to be the hypotenuse of the triangle and hence we use the Pythagoras theorem to find the displacement given by path $PR$. From Pythagoras theorem we have:
$P{R^2} = {\left( {PQ} \right)^2} + {\left( {QR} \right)^2}$
We are already given the distances from $P$ to $Q$ and $Q$ to $R$ as $8cm$ and $6cm$ respectively. Hence we substitute these values to get:
$P{R^2} = {\left( 8 \right)^2} + {\left( 6 \right)^2}$
By further solving we get:
$P{R^2} = 64 + 36$
$ \Rightarrow P{R^2} = 100$
By taking square root on both sides we have:
$ \Rightarrow PR = \sqrt {100} $
$ \therefore PR = 10\,cm$
We consider the positive value of displacement and hence the resultant displacement of the ant is $10\,cm$.

Note:Even-though distance and displacement seem to be similar, they differ from each other in accordance to their concepts. This may be a common confusion as distance is often referred to as displacement as well. There may be certain situations where the distance is equivalent to the displacement as well and this happens when an object’s paths are the same. For example, an object that travels along a straight line of motion and in the same direction has the same value of distance and displacement. Since, distance is a scalar quantity the distance value is always said to be zero or positive but displacement can have negative values as well.