Question

A well of inner diameter 14 meter dug to a depth of 15 meter. Earth taken out of it has been evenly spread all around it to a width of 7 meter to form an embankment. Find the height of the embankment so formed.

Answer 1

Hint: In this question we only use some of the basic formula of the cylinder and as the question says we will have to find the height of the cylinder or embankment. Here, the volume of the embankment is equal to the volume of the earth dug out. So, we will first try to find the volume of the well.

Complete step-by-step answer:

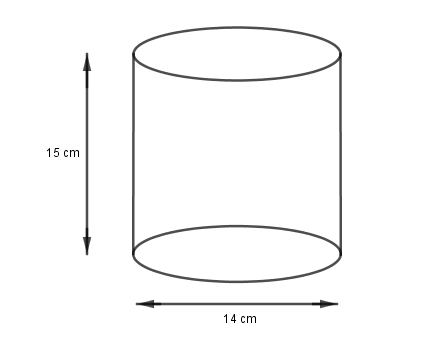
Let ‘h’ be the height of the wall.
‘r’ be the radius of the wall.
h = 15m, r = $ \dfrac{{14}}{2} $ = 7 cm (Diameter is twice of radius)
Now, Volume of the earth dug out from well = $ \pi {r^2}h $
Putting the values:
 $ \Rightarrow \dfrac{{22}}{7} \times 7 \times 7 \times 15 $ (Shape of well is similar to cylinder)
\[ \Rightarrow 2310\,{{\text{m}}^3}\]
Now, Let the height of the embankment = ‘H’

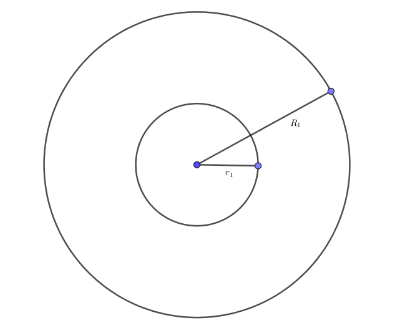
From the question, it is clear from the diagram that the embankment forms a cylindrical shell whose inner radius ( $ {r_1} $ ) = 7 meter and external radius $ ({R_1}) $ = 7 + 7 = 14 meter.
So, we can not say the volume of embankment is equal to the volume of earth dug out.
From the above statement we can say that:
Volume of embankment = Volume of earth dug out
 $
   \Rightarrow \pi \left[ {{R^2}_1 - {r^2}_1} \right]H = 2310 \\
   \Rightarrow \pi \left[ {{{14}^2} - {7^2}} \right]H = 2310 \\
  $
 $
   \Rightarrow \pi \left[ {196 - 47} \right]H = 2310 \\
   \Rightarrow \pi \times 147 \times H = 2310 \\
   \Rightarrow H = \dfrac{{2310 \times 7}}{{147 \times 22}} \\
   \Rightarrow H = \dfrac{{16170}}{{3234}} = 5{\text{m}} \;
  $
Hence, the height of the embankment is $5$ meters.
So, the correct answer is “ $5$ meters”.

Note: In the above question we used the volume of the cylinder to find the height of the embankment. First, we find the volume of earth dug which is in the form of a cylinder that’s why we use the formula $ \pi {r^2}h $ . After that we can say that volume of earth dug out and volume of embankment is the same because the same amount of earth has spread around the well. Students can make sure that they put the correct value of the measurements so that they can get a correct answer