Question

A well of diameter 3m is dug 14m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4m to form an embankment. Find the height of the embankment.

Answer 1

Hint: we have to identify that both the well dug and circular ring embankment formed are in the shape of a cylinder but embankment is cylinder with internal radius and external radius and we have to know the formulae for volume of cylinder=\[\pi {{r}^{2}}h\]

Complete step-by-step answer:

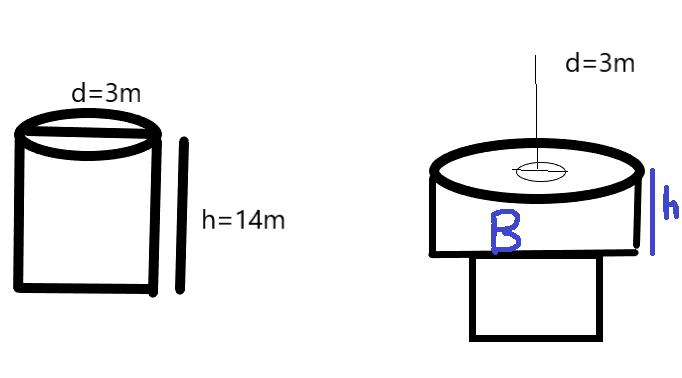
Given a well is dug which is of 3m diameter and 14m deep and it is used to form a circular ring of width 4m to form a embankment
Both well and embankment are in the shape of a cylinder.
Let well be cylinder A and embankment be cylinder B
Since mud of well is distributed in embankment
Volume of well=volume of embankment
Volume of well
For cylinder A,
Diameter=3m
So, radius =r=3/2m=1.5m
Height =14m
Volume of cylinder A= \[\pi {{r}^{2}}h\]
\[=\pi \times {{\left( 1.5 \right)}^{2}}\times 14\]
\[=\pi \times 2.25\times 14\]
\[=31.5\pi {{m}^{3}}\]
So volume of well =volume of cylinder A = \[=31.5\pi {{m}^{3}}\]
Volume of embankment
For cylinder B
Cylinder B is a hollow cylinder with inner diameter = diameter of well=3m
Internal radius \[=\] \[^{\mathop{r}_{1}}=\dfrac{3}{2}=1.5m\]
External radius \[=\] \[\mathop{r}_{2}=1.5+4=5.5m\]
Volume of cylinder with internal radius \[=\pi {{\mathop{r}_{1}}^{2}}h\]
\[=\pi h{{\left( 1.5 \right)}^{2}}\]
Volume of cylinder with external radius \[=\pi {{\mathop{r}_{2}}^{2}}h\]
\[=\pi h{{\left( 5.5 \right)}^{2}}\]
Volume of cylinder B=volume of cylinder with external radius -volume of cylinder with internal radius
\[=\pi h{{\left( 1.5 \right)}^{2}}\]\[-\pi h{{\left( 1.5 \right)}^{2}}\]
\[=\pi h\left( 30.25-2.25 \right)\]
\[=\pi h(28)\]
\[=28\pi h{{m}^{3}}\]
So, volume of embankment\[=28\pi h{{m}^{3}}\]
Now,
Volume of well=volume of embankment
\[31.5\pi =28\pi h\]
\[h=\dfrac{31.5}{28}\]
\[h=1.125\]
Hence, height of embankment\[=1.125m\]

Note: They have given that earth taken out of it has been spread evenly all around it so volume from which it has dug and volume of new embankment formed are equal. There are so many problems of this type and students have to equate the volume of old shape and volume of new shape formed.