Question

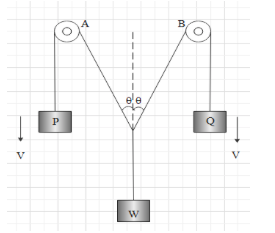
A weight W is tied to two strings passing over the frictionless pulleys A and B as shown in the figure. If weights P and Q move downwards with speed V, the weight W at any instant rises with the speed:

A. $V\cos \theta $
B. $2V\cos \theta $
C. $\dfrac{V}{{\cos \theta }}$
D. $\dfrac{{2V}}{{\cos \theta }}$

Answer 1

Hint-In the given figure we can consider a right triangle connecting one of the pulleys, the midpoint of line joining the two pulleys and point of suspension of weight W. Using Pythagoras theorem, we will get an equation relating length of the string and height to which weight can be raised. By differentiating this equation with respect to time we can find the velocity with which the weight moves upward.

Step by step solution:
It is given that a weight is tied to two strings passing over two frictionless pulleys. If weights P and Q move downwards with a speed V, the weight W Rises upward. We need to find the speed with which weight W rises upward.
Consider the triangle BOS shown in the figure below.

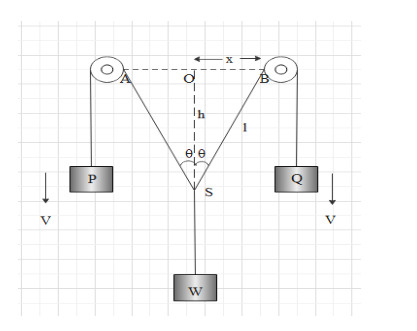
Since it is a right-angled triangle, we can use the Pythagoras theorem.
 let the length of the string be l. Then we can write
${l^2} = {h^2} + {x^2}$
Let us differentiate this equation with respect to t.
$ \Rightarrow 2l\dfrac{{dl}}{{dt}} = 2h\dfrac{{dh}}{{dt}} + 0$..............(1)
We know that the rate of change of distance is velocity. Hence, we can write
$\dfrac{{dl}}{{dt}} = V$
Substituting this in equation 1 we get
$ \Rightarrow 2l \times V = 2h\dfrac{{dh}}{{dt}} + 0$.................(2)
The rate of change of the height h will give us the velocity of the block upwards. Let this velocity be denoted as u.
$ \Rightarrow \dfrac{{dh}}{{dt}} = u$
Thus equation 2 becomes
$ \Rightarrow 2lV = 2hu$
$ \Rightarrow u = \dfrac{{lV}}{h}$
$ \Rightarrow u = \dfrac{V}{{\dfrac{h}{l}}}$
From the triangle BOS, we can find that the value of $\cos \theta $ is given as
$\cos \theta = \dfrac{{{\text{adjacent}}\,{\text{side}}}}{{{\text{hypotenuse}}}}$
$ \Rightarrow \cos \theta = \dfrac{h}{l}$
Thus, we can substitute $\cos \theta $ instead of $\dfrac{h}{l}$
Using this we get the value of velocity u as
$\therefore u = \dfrac{V}{{\cos \theta }}$

So, the correct option is option C.

Note:Remember that while taking the derivative of equation ${l^2} = {h^2} + {x^2}$ , the derivative of x with respect to time will be zero. This is because the value of x is a constant. Its value does not change with time. So, its derivative with respect to time will be zero.