Question

A weight $Mg$ is suspended from the middle of a rope whose ends are at the same level. The rope is no longer horizontal. The minimum tension required to completely straighten the rope is
A. $\dfrac{{Mg}}{2}$
B. $Mg\cos \theta $
C. $2Mg\cos \theta $
D. Infinitely large

Answer 1

Hint: We need to draw a figure showing all the components of the force acting on the weight suspended so that we do not miss out on any component and then equate the opposite forces and find the expression for the minimum tension required to straighten the rope.

Complete step by step solution:
Let us first draw a diagram to get a better understanding of the situation.

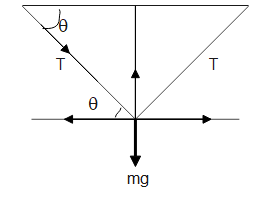
The tension is due to the weight suspended from the middle of the rope. The tension can be resolved into two components $T\cos \theta $ and $T\sin \theta $ where $\theta $ is the angle which the rope makes with the horizontal when the weight is suspended on it.
By equating the components of force in the opposite direction we can write
$2T\sin \theta = mg$
$ \Rightarrow T = \dfrac{{mg}}{{2\sin \theta }}$
When the $\theta = 0^\circ $, then the rope will be straight. Therefore to bring back the rope to a straight position we will have to angle zero.
Substituting the value we get,
$ \Rightarrow T = \dfrac{{mg}}{{2\sin 0}}$
$ \Rightarrow T = \infty $
This denotes that the minimum tension required to straighten the rope with weight suspended is infinite.
Therefore option D) is correct.

Note: When an object is suspended from a rope the force components acting on it will be balanced by each other. The vertical component of the tension will be balanced by the weight of the suspended object. Since there are two components of tension from either side in the vertical direction, factor 2 is multiplied by the vertical component. The forces are balanced when the system is in equilibrium. The amount of tension required to straighten the rope does not depend on the weight suspended at the midpoint of the rope.