Question

A wedge of masses m₂ is kept on a spring balance. A small block of mass m₁ can move along the frictionless incline of the wedge. What is the reading of the balance while the block slides? Ignore the recoil of the wedge.

Answer 1

Hint: Wedges are used to lift heavy objects, separating them from the surface upon which they rest. Consider a block that is to be lifted by a wedge. As the wedge slides under the block, the block slides up the sloped side of a wedge. This lifts the weight FB of the block.
Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting upon an object in a given situation. A free-body diagram is a special example of the vector diagrams that were discussed in an earlier unit. These diagrams will be used throughout our study of physics.

Complete step by step solution:

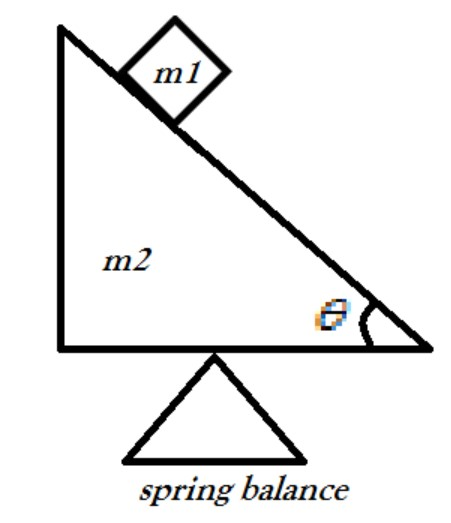
The above diagram is constructed as per the question.
Now,
Drawing a free body diagram of mass m₁ and resolving the force into its components.

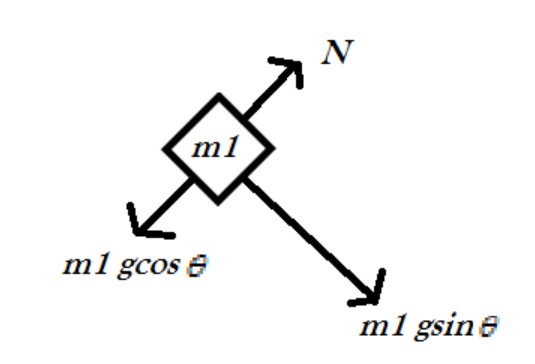
Here, N represents the Normal component, g represents the acceleration due to gravity.
Since the mass m₁ remains in contact therefore $N = m_1 \times g\cos \theta $
Now,
Drawing the free body diagram of the wedge,

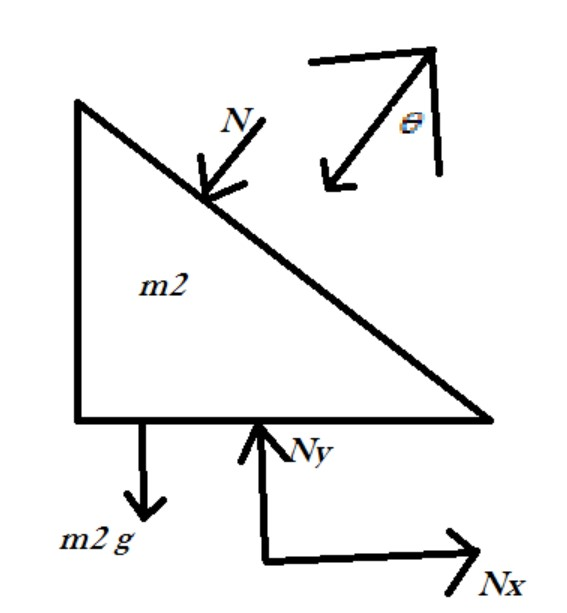
So, clearly from the above and by balancing all the forces, we can write,
\[
  Ny = (m_2 \times g) + (N\cos \theta ) \\
  Ny = (m_2 \times g) + (m_1g\cos \theta \times \cos \theta ) \\
  Ny = (m_2 \times g) + (m_1g{\cos ^2}\theta ) \\
\]
And, by balancing forces in X direction we can write,
$
  Nx = N\sin \theta \\
  Nx = m_1g\cos \theta \sin \theta \\
$
Now, since we know that weight balance only reads upward normal force, therefore it will only read Ny.
Thus,
 $
  Ny = m_2g + m_1g(1 - {\sin ^2}\theta ) \\
  Ny = g(m_2 + m_1) - m_1g{\sin ^2}\theta \\
$

Hence the reading of the spring balance will be $ = g(m_2 + m_1) - m_1g{\sin ^2}\theta $

Note: In problems of wedge and block always try to draw the free body diagram and try to resolve the components and then proceed. This will always help you in solving problems easily and avoiding any confusions.