Question

A water tank placed on the floor has two small holes, pinched in the vertical wall one above the other. The holes are $3.3cm$ and $4.7cm$ above the floor. If the jets of water issuing out from the holes hit the floor at the same point on the floor, then the height of the water in the tank is

A. $3cm$
B. $6cm$
C. $8cm$
D. $9cm$

Answer 1

Hint: Given that the water tank is filled with water, then water will have a free surface. The free surface in a liquid means the upper surface of the liquid that is in contact with the air. If the free surface of a liquid is disturbed, then the waves are formed on the surface of the liquid.

Complete answer:
Step I:
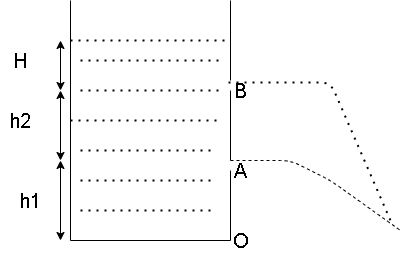
Let A be the first hole and B is the second hole on the tank and let O be the bottom of the tank. Then given is
$OA = 3.3cm$ and $OB = 4.7cm$
Let H be the total height upto which the water is filled in the tank. The velocity of a liquid falling from a height on the ground is given by
$V = \sqrt {2gH} $
Where H is the height of the liquid falling from the top part of the tank.
Therefore, for the first hole, height is $ = H - 3.3$
${V_1} = \sqrt {2g(H - 3.3)} $
Step II:
Therefore, the time taken for the water to drop at the ground is given by its time of flight.
Formula for time of flight is, $T = \sqrt {\dfrac{{2h}}{g}} $
Where h is the height taken from the bottom of the tank.
Hence for the first hole, time of flight is
${T_1} = \sqrt {\dfrac{{2{h_1}}}{g}} $
Or \[\sqrt {\dfrac{{2 \times 3.3}}{g}} = \sqrt {\dfrac{{6.6}}{g}} \]
Step III:
Horizontal range is the horizontal distance travelled by the liquid or water. The formula is
$x = v.t$
For first hole, ${x_1} = {v_1}.{t_1}$
$ = \sqrt {2g(H - 3.3)} .\sqrt {\dfrac{{6.6}}{g}} $
=$\sqrt {[13.2(H - 3.3)]} $
Step IV:
Similarly for the second hole, velocity of the water falling on the ground is, ${v_2} = \sqrt {2g(H - 4.7)} $
Time of flight for the second hole is,]${t_2} = \sqrt {\dfrac{{2 \times 4.7}}{g}} $
Or${t_2} = \sqrt {\dfrac{{9.4}}{g}} $
Horizontal range for second hole, x2 = v2. T2${x_2} = {v_2}.{t_2}$
$ = \sqrt {2 \times 9.4(H - 4.7)} $
Step V:
Also it is given that water hits at the same point on the floor. Therefore,
${x_1} = {x_2}$
Squaring both sides, the equation becomes
$13.2(H - 3.3) = 18.8(H - 4.7)$
$33H - 108.9 = 47H - 220.9$
$14H = 112$
$H = 8cm$

Therefore, Option (C) is the right answer.

Note:
Since the jet of water is falling from the hole in the tank, so it is an example of horizontal projectile. If a body is made to fall in a horizontal direction from a certain height with a certain velocity then it is said to be in a horizontal projectile motion. This motion is said to be an accelerated motion and is controlled by gravity.