Question

A wall of length 10 m was to be built across an open ground. The height of the wall is 4 m and the thickness of the wall is 24 cm. If this wall is to be built up with bricks whose dimensions are $24cm \times 12cm \times 8cm$. How many bricks would be required?

Answer 1

Hint: We will first find the volume of the wall using the formula, $l \times b \times h$, where $l$ is the height of the wall, $b$ is the breadth of the wall and $h$ is the height of wall. Similarly, find the volume of the brick. Then, divide the volume of the wall by the volume of the brick to find the number of bricks.

Complete step-by-step answer:
We are given that the length of the wall is 10m, the breadth of the wall is 24 cm and the height of the wall is 4m.

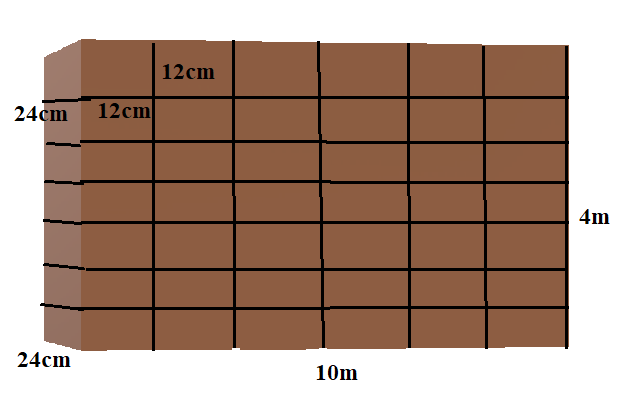
We will first calculate the value of the wall.
Wall is in the shape of the cuboid.
The volume of the cuboid is $l \times b \times h$, where $l$ is the height of the wall, $b$ is the breadth of the wall and $h$ is the height of the wall.
But, thickness of the wall is 24cm, we will convert it into m by dividing it by 100,
$\Rightarrow$ $\dfrac{{24}}{{100}} = 0.24m$
Hence, the volume of the wall is $10 \times 4 \times 0.24{m^3}$
Similarly, we will find the volume of the brick which is $24 \times 12 \times 8c{m^3}$
But, we will convert $c{m^3}$ into \[{m^3}\] by dividing it by ${100^3}$
Then, the volume of one brick is $\dfrac{{24 \times 12 \times 8}}{{{{100}^3}}}{m^3}$
To find the number of bricks, we will divide the volume of the wall by volume of each brick.
$\Rightarrow$ $\dfrac{{10 \times 4 \times 0.24{m^3}}}{{\dfrac{{24 \times 12 \times 8}}{{{{100}^3}}}{m^3}}} = \dfrac{{10 \times 4 \times 0.24 \times {{100}^3}}}{{24 \times 12 \times 8}}$
On simplifying the above expression, we will get,
$\Rightarrow$ $\dfrac{{10 \times 4 \times 0.24 \times {{100}^3}}}{{24 \times 12 \times 8}} = 4166.67$
Hence, the number of bricks is 4166 in the wall.

Note: We have converted the volume of brick in ${m^3}$, but one can also solve the given question by converting the volume of the wall in $c{m^3}$. The volume of any object gives the space enclosed by the object. Volume is always measured in cubic units.