Question

A villager Ramayya has a plot of land in the shape of a quadrilateral. The gram panchayat of the village decided to take over some portion of his plot from one of the corners to construct a school. Ramayya agrees to the above proposal with the condition that he should be given an equal amount of land in exchange of his land adjoining his plot so as to form a triangular plot. Explain how his proposal will be implemented.

Answer 1

Hint: In order to solve the above problem first we will make the diagram of the problem statement. Then we need to prove the old area of land is the same as the new area of land. Use the property of parallelogram that triangles formed on the parallelogram with the same base and between the same parallel lines are equal in area.

Complete step-by-step answer:

Let us solve the problem with the help of the following diagram

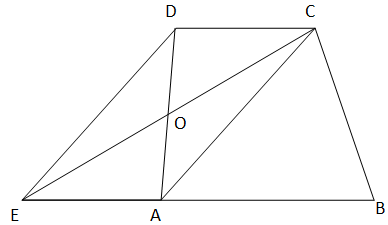
Let quadrilateral ABCD be the original shape of the field owned by Ramayya.
Let us join AC and draw \[DE||AC\] joining CE and EA.

Let gram panchayat construct its school in ar(EDC) by taking land ODC.

So Ramayya gives up ODC and takes adjacent land OEA in return.
Now, he has the land EBC.

So, we need to prove that Area of old land = Area of new land

We need to prove ar(ABCD)=ar(EBC)
As we have taken \[DE||AC\& DE = AC\]

So ACDE is a parallelogram
For triangles ACD and ACE

Both the triangles have the same base that is AC. And also they lie between sets of two parallel lines AC and DE.

As we know that triangles with the same base and between the same parallel lines are equal in area, so we have
$\therefore ar\left( {ACD} \right) = ar\left( {ACE} \right)$ ---(1)

Adding $ar\left( {ABC} \right)$ on both the sides of the equation we get:
$
   \Rightarrow ar\left( {ACD} \right) + ar\left( {ABC} \right) = ar\left( {ACE} \right) + ar\left( {ABC} \right) \\
   \Rightarrow ar\left( {ABCD} \right) = ar\left( {EBC} \right){\text{ }}\left[ {{\text{from the figure}}} \right] \\
 $

Hence, now the area of land with ramayya is triangular and also the area of land is same as it was earlier.

Note: The problem can be solved in another way as well by considering some different shapes of quadrilaterals and triangles of different shapes. But the most important step is to construct a figure and visualize the practical problem with some geometrical figures. Also students must remember the properties of parallelogram one of which is mentioned in the solution.