Question

A vessel is in the form of an inverted cone. Its height is 8cm and the radius of its top, which is open, is 5cm. it is filled with water up to the brim, when lead shots, each one of which is a sphere of radius 0.5cm are dropped into the vessel, one fourth of the water flows out. Find the number of lead shots dropped in the vessel.

Answer 1

Hint: Here, we will first find out the volume of the vessel and then the volume of the lead shots which were dropped in the vessel. We will apply the formula:
Number of lead shots = volume of the water that flows out after leads are dropped in the vessel/volume of 1 lead shot.

Complete step-by-step answer:
First let us consider the figure which can be drawn from the given details.

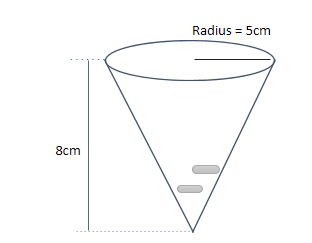
We are given that radius of the inverted cone is: r= 5cm and, height h= 8cm
Also, the volume of the water flown out= $\dfrac{1}{4}$( volume of the cone)
We know that volume of the cone is $V = \dfrac{1}{3}\pi {r^2}h$
$
   \Rightarrow V = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 5 \times 5 \times 8 \\
   \Rightarrow V = \dfrac{{4400}}{{21}}c{m^3} \\
 $
For calculation of the volume of the water flown out,
Volume of the water flown out= $\dfrac{1}{4}$( volume of the cone) = $\dfrac{1}{4} \times \dfrac{{4400}}{{21}}$
$ \Rightarrow $volume of the water flown out= $\dfrac{{1100}}{{21}}c{m^3}$
We are given that lead shots are in the shape of spheres with radius r= 0.5cm
   $\therefore $volume of 1 lead shot = volume of the sphere= $\dfrac{4}{3}\pi {r^3}$
$
   \Rightarrow v = \dfrac{4}{3} \times \dfrac{{22}}{7} \times {(0.5)^3} \\
   \Rightarrow v = \dfrac{{11}}{{21}}c{m^3} \\
 $
Hence, the number of lead shots = volume of the water that flows out after leads are dropped in the vessel/volume of 1 lead shot
$ \Rightarrow $no. of lead shots = $\dfrac{{\dfrac{{1100}}{{21}}}}{{\dfrac{{11}}{{21}}}} = \dfrac{{1100}}{{21}} \times \dfrac{{21}}{{11}} = 100$
Therefore, the total number of lead shots dropped in the vessel are 100.

Note: In such problems, you may get confused between the given information about which formula you need to apply and you may go wrong while solving for the total number of lead shots from the volume of displaced water and lead shots. Here, we have used the formula that the volume flown out of the vessel is equal to the number of lead shots dropped since only that much amount of water is displaced, the much volume shots occupy.