Question

A vessel is filled with liquid 3 parts of which are water and 5 parts syrup. How much of the mixture must be drawn off and replaced with water so that the mixture may be half water and half syrup?

Answer 1

Hint: We will start solving this question by taking the amount of mixture to be replaced by x of 8 litres. Then, we will make a linear equation and apply the condition given in the question to find the value of x.

Complete step-by-step answer:
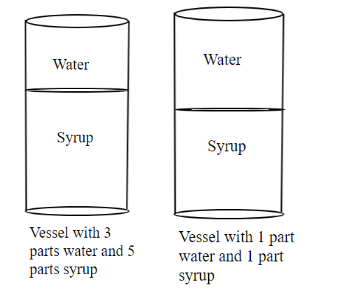
Now, we have 3 parts of water and 5 parts of syrup in a mixture. Total amount of mixture = 8 litres.
So, amount of water in the mixture = $ \dfrac{3}{8} $ litres
Similarly, the amount of syrup in the mixture = $ \dfrac{5}{8} $ litres.
 

Now, let x litres of total mixture be replaced by water.
So, according to the question, amount of water in the new mixture = $ \left( {3 - \dfrac{{3x}}{8} + x} \right) $ litres
Amount of syrup in the new mixture = $ \left( {5 - \dfrac{{5x}}{8}} \right) $ litres.
According to question, amount of water = amount of syrup
So, we have, $ 3 - \dfrac{{3x}}{8} + x = 5 - \dfrac{{5x}}{8} $
Solving the above expression, we get
\[2 = \dfrac{{5x}}{8} - \dfrac{{3x}}{8} + x\]
\[2 = \dfrac{{2x}}{8} + x\]
 $ 2 = \dfrac{{5x}}{4} $
 $ x = \dfrac{8}{5} $
So, part of mixture replaced = $ \left( {\dfrac{8}{5} \times \dfrac{1}{8}} \right) $ = $ \dfrac{1}{5} $ .
Note: Whenever we come up with such types of questions, we will let the quantity to be found be x (variable). After taking the variable, we will use all the conditions given in the question to make a linear equation with one variable. After making the equation, we will solve the equation to find the value of the variable. Now, with the help of variables, we find the solution to the given problem.