Question

A vessel contains water up to a height of $20cm$ and above it an oil up to another $20cm$. The refractive indices of the water and the oil are $1.33$ and $1.30$ respectively. Find the apparent depth of the vessel when viewed from above.

Answer 1

Hint: Refractive index is the ratio of real depth to the apparent depth. So, in order to find the apparent depth, we will rearrange the equation for the refractive index. Then, by putting the value of the refractive index of the two liquids and their real depth, we will find the answer.

Complete answer:
The diagram for this question:

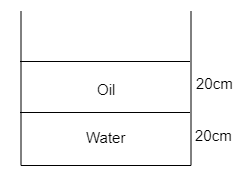
We know that the refractive index can also be defined as the ratio of real depth of an object to the apparent depth of the same object. So, we can say that,
$\mu = \dfrac{h}{{{h^{'}}}}$
Where,
$\mu $ is the refractive index of the medium
$h$ is the real depth at which the object is present, and
${h^{'}}$ is the apparent depth at which the object appears to be present.
This relation can also be written as,
${h^{'}} = \dfrac{h}{\mu }.....(1)$
So, according to the above equation, the apparent depth of an object can be defined as the ratio of real depth of the object to the refractive index of the medium.
In this question we are given two mediums and hence, we have two refractive index and two depths.
Let ${h_1}$ be the real depth of water and let ${h_2}$ be the real depth of oil. Similarly, let ${\mu _1}$ be the refractive index of the water and let ${\mu _2}$ be the refractive index of the oil. So, the expression for the apparent depth ${h^{'}}$ is,
${h^{'}} = \dfrac{{{h_1}}}{{{\mu _1}}} + \dfrac{{{h_2}}}{{{\mu _2}}}......(1)$ (from equation 1)
In this question,
${h_1} = 20cm$,
 ${h_2} = 20cm$,
${\mu _1} = 1.33$,
${\mu _2} = 1.30$
On putting the above values in equation (2), we get,
${h^{'}} = \dfrac{{20}}{{1.33}} + \dfrac{{20}}{{1.30}}$
${h^{'}} = 15.03 + 15.38$
${h^{'}} = 30.41cm$
So, the apparent depth of the vessel when viewed from above is ${h^{'}} = 30.41cm$
Note: When any object is placed in a denser medium and when it is viewed from a rarer medium, then it appears to be at a depth less than the real depth. For example, when an object is kept in water, then it seems to be slightly raised. This phenomenon occurs due to refraction of light. As the light travels from a denser medium to a rarer medium, so this phenomenon happens.