Question

A vessel contains oil (density d) over mercury (density D). A homogeneous solid sphere floats with half of its volume in mercury and the other half in the oil. The density of the material of the sphere is :
A. $\sqrt {Dd} $
B. $\dfrac{{2Dd}}{{D + d}}$
C. $\dfrac{{D + d}}{2}$
D. $\dfrac{{Dd}}{{D + d}}$

Answer 1

Hint:The sphere is in equilibrium, with half of its volume in Mercury and the other half in oil. Therefore the weight of the sphere is balanced by the force of buoyancy exerted by oil and mercury. The force of buoyancy on any object is given as $F = \rho Vg$, where ρ is the density of liquid, V is the volume submerged.

Complete step by step answer:
Archimedes' principle states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially submerged, is equal to the weight of the fluid that the body displaces.

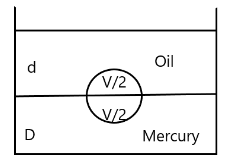
Therefore the force of buoyancy due to oil is ${B_{oil}} = \dfrac{V}{2}dg$.
And the force of buoyancy due to Mercury is ${B_{mercury}} = \dfrac{V}{2}Dg$.
The weight of the sphere is balanced by the force of buoyancy due to oil and mercury and therefore we can write,
$W = {B_{oil}} + {B_{mercury}}$ ------------(1)
We know that the density is defined as the ratio of mass to volume $\rho = \dfrac{m}{V}$.
Therefore the mass of the sphere is$m = \rho V$. So we get the weight of the sphere as $W = mg = \rho Vg$.
Substituting the given values in the equation we get,
$
\rho Vg = \dfrac{V}{2}dg + \dfrac{V}{2}Dg \\
\therefore\rho = \dfrac{{d + D}}{2} \\ $
Therefore the density of the material of the sphere is $\rho = \dfrac{{d + D}}{2}$.

Hence, option C is the correct answer.

Note: One should know the general formula force of buoyancy $F = \rho Vg$. In the formula the density of the liquid is to be taken and not the density of the material of the sphere. Students should keep this point in mind to avoid errors in answers. According to Archimedes principle for an object to float the weight of the displaced liquid is balanced by the weight of the object.