Question

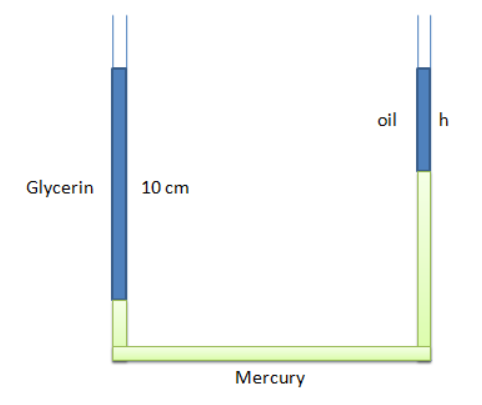
A vertical U-tube of uniform cross-section contains mercury in both sides of its arms as shown below. A Glycerin column of $10{\text{ cm}}$ is introduced into one of its arms. Oil of density ${\text{0}}{\text{.8 g/cc}}$is poured into the other arm until the upper surface of the oil and glycerin are at the same horizontal level.$({\rho _{gh}} = 13.6g/cc,{\rho _{glycerine}} = 1.3g/cc)$
The length of the column is
A.$10.4{\text{ cm}}$
B.${\text{8}}{\text{.2 cm}}$
C.$7.2{\text{ cm}}$
D.${\text{9}}{\text{.6 cm}}$

Answer 1

Hint: This question can be solved by using Pascal’s law that is the pressure is the same throughout the entire enclosed liquid. To solve this question, first, find the pressure at both the bottom level of the glycerin and the separation between the oil and the horizontal level of glycerin. Then by using the law that pressure is equal, equate both the equations to find the height of the column of oil.
Formula used: $P = \rho gh$

Complete answer:

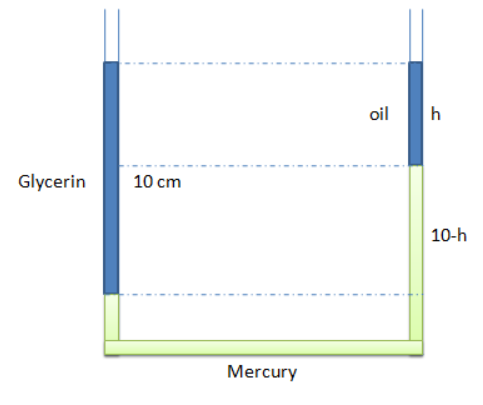
Let the length of the oil column be h.
We know the length of the glycerin column is $10{\text{ cm}}{\text{.}}$
Therefore $10{\text{ - h}}$will be the length of the column between the horizontal level of glycerin and oil.
Now calculate the pressure at the lower bottom of the glycerin.
So the pressure at this point will be the sum of the atmospheric pressure and the pressure of the glycerin.
This is found by using the formula $P = \rho gh$
Where P is the pressure, g is the acceleration due to gravity, rho is the density and h is the height of the column.
Therefore the pressure at the point is
$P = {P_o} + {\rho _{glycerin}}gh$
Now calculate the pressure at the lower bottom of the separation between the oil and the horizontal level of glycerin.
So the pressure at this point will be the sum of the atmospheric pressure, the pressure of the oil, and the pressure of the mercury.
This is found by using the formula $P = \rho gh$
Where $P$ is the pressure, \[g\] is the acceleration due to gravity, $\rho $ is the density, and \[h\] is the height of the column.
Therefore the pressure at the point is,
$P = {P_o} + {\rho _{mercury}}g(10 - h) + {P_{oil}}gh$
Now, we know that pressures at both these points are equal.
Therefore we get,
${P_o} + {\rho _{glycerin}}gh = {P_o} + {\rho _{mercury}}g(10 - h) + {P_{oil}}gh$
By canceling the like terms we get,
${\rho _{glycerin}}{h_{glycerin}} = {\rho _{mercury}}(10 - {h_{oil}}) + {P_{oil}}{h_{oil}}$
By substituting the values of density and height of column we get,
$1.3 \times 10 = 13.6 \times (10 - {h_{oil}}) + 0.8 \times {h_{oil}}$
Rearranging and simplifying we get,
$ \Rightarrow 13 = 13.6 \times (10 - {h_{oil}}) + 0.8 \times {h_{oil}}$
$ \Rightarrow 13 = 136 - 13.6 \times {h_{oil}} + 0.8 \times {h_{oil}}$
$ \Rightarrow 123 = 12.8{h_{oil}}$
$ \Rightarrow {h_{oil}} = \dfrac{{123}}{{12.8}} = 9.6$

Correct answer is Option (C).

Note:
According to Pascal’s law, a change in pressure applied to an enclosed liquid transmits it undiminished. In other words, pressure is the same throughout the entire enclosed liquid. In other words, pressure is the same throughout the entire enclosed liquid. This principle of Pascal’s law is applied in the case of hydraulic jacks. It is a device that lifts up objects such as a car.