Question

A vertical $U-$tube has two liquid $1$ and $2$. The height of liquids columns in both the limbs are $h$ and $2h$, as shown in the figure. If the density of the liquid $1$ is $2\rho $.

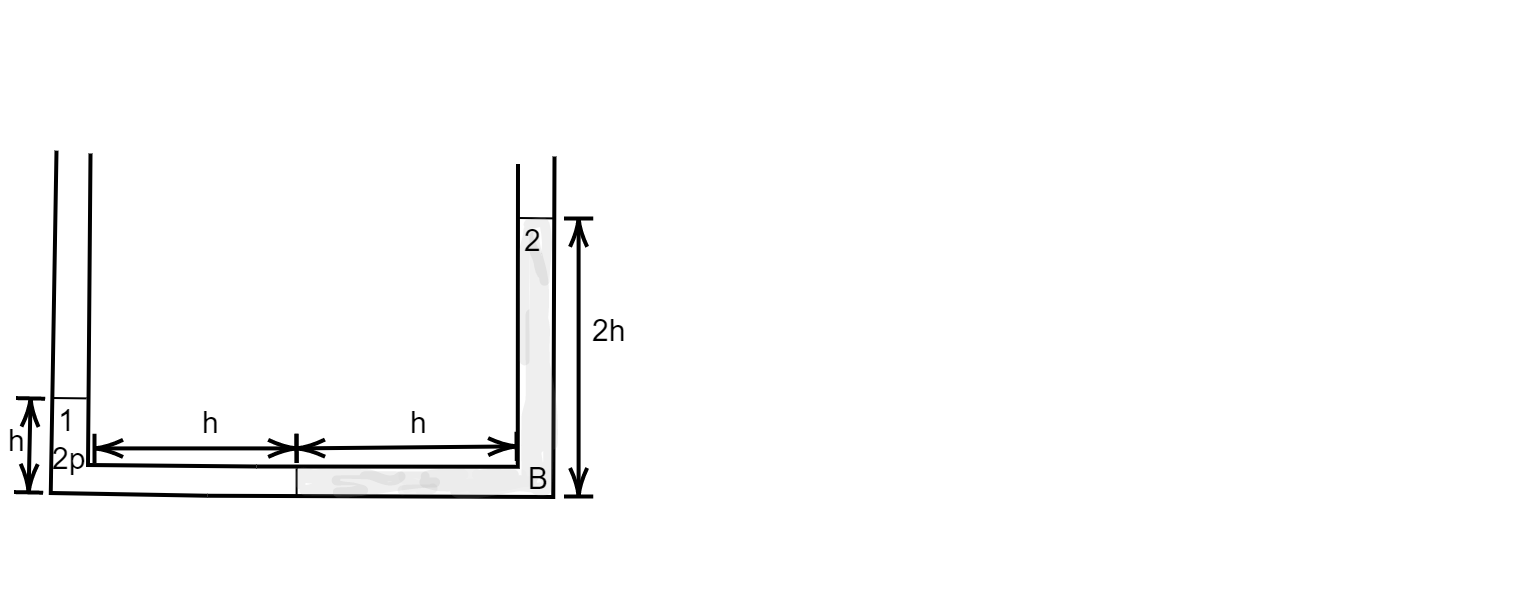
A.Find the density of liquid $2$.
B.If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.

Answer 1

Hint: To solve this question which involves a vertical $U-$tube, we have to assume two points in each liquid which is at the same level and then their pressure will also be equal. Therefore, by using this concept we can solve the given question easily.

Complete answer:
A.Let us assume two points $A$ and $B$ at the bottom of the vertical $U-$tube. As given in the first part that the vertical $U-$tube that has two liquid $1$ and $2$ is stationary hence we can conclude that the pressure at both the points will be the same. Keeping in mind that the density of the liquid $1$ is $2\rho $, we can write down the equation as:
$\begin{align}
  & {{P}_{A}}={{P}_{B}} \\
 & \Rightarrow {{P}_{0}}+\left( 2\rho \right)gh={{P}_{0}}+dg\left( 2h \right) \\
 & \Rightarrow \left( 2\rho \right)gh=dg\left( 2h \right) \\
 & \therefore d=\rho \\
\end{align}$
B.Thus, the density of the liquid $2$ is $\rho $.

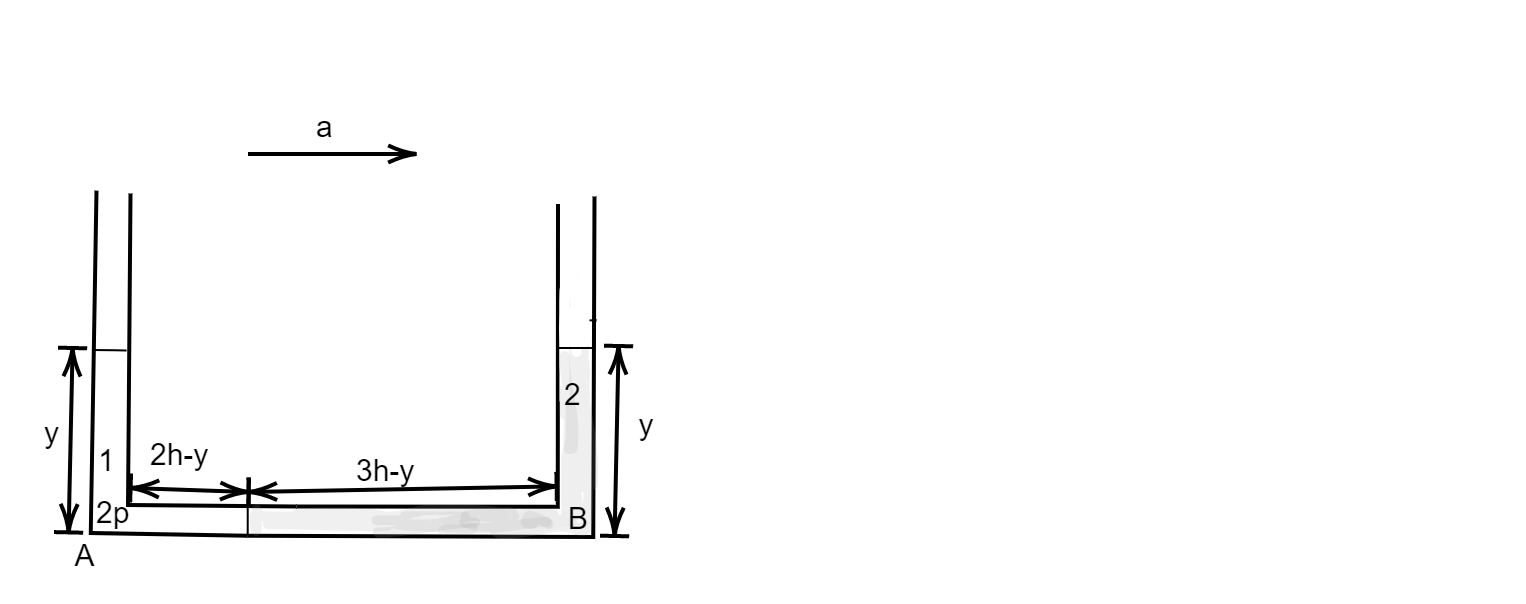
Now, if we accelerate the tube towards right till the heights of liquid columns will be the same. Let us consider this height be $l$, then the length of liquid $1$ in the horizontal section will be $\left( 2h-l \right)$ and the length of liquid $2$ in the horizontal section will be $\left( 3h-l \right)$. The total length of the horizontal section will not change hence:
$\begin{align}
  & 2h=\left( 2h-l \right)+\left( 3h-l \right) \\
 & \Rightarrow 2h=5h-2l \\
 & \Rightarrow 2l=5h-2h \\
 & \Rightarrow 2l=3h \\
 & \Rightarrow l=\dfrac{3h}{2} \\
\end{align}$
The length of liquid $1$ in the horizontal section will be:
$\begin{align}
  & 2h-\dfrac{3h}{2} \\
 & \Rightarrow \dfrac{h}{2} \\
\end{align}$
The length of liquid $2$ in the horizontal section will be:
$\begin{align}
  & 3h-\dfrac{3h}{2} \\
 & \Rightarrow \dfrac{3h}{2} \\
\end{align}$
Now, the pressure at the interface of the two liquids will be:
$P'={{P}_{A}}-\left( 2\rho \right)a\left( \dfrac{h}{2} \right)$
Here, ${{P}_{A}}={{P}_{0}}+\left( 2\rho \right)g\left( \dfrac{3h}{2} \right)$
On substituting we get:
$\begin{align}
  & P'={{P}_{0}}+\left( 2\rho \right)g\left( \dfrac{3h}{2} \right)-\left( 2\rho \right)a\left( \dfrac{h}{2} \right) \\
 & \Rightarrow P'={{P}_{0}}+3\rho gh-\rho ah \\
\end{align}$
Also, $P'={{P}_{B}}+\rho a\left( \dfrac{3h}{2} \right)$ and ${{P}_{B}}={{P}_{0}}+\rho g\left( \dfrac{3h}{2} \right)$, therefore:
$\begin{align}
  & P'={{P}_{0}}+\rho g\left( \dfrac{3h}{2} \right)+\rho a\left( \dfrac{3h}{2} \right) \\
 & \Rightarrow {{P}_{0}}+3\rho gh-\rho a={{P}_{0}}+\rho g\left( \dfrac{3h}{2} \right)+\rho a\left( \dfrac{3h}{2} \right) \\
 & \Rightarrow 3\rho gh-\rho a=\rho g\left( \dfrac{3h}{2} \right)+\rho a\left( \dfrac{3h}{2} \right) \\
 & \Rightarrow 3\rho gh-\rho g\left( \dfrac{3h}{2} \right)=\rho a\left( \dfrac{3h}{2} \right)+\rho a \\
 & \Rightarrow \rho g\left( \dfrac{3h}{2} \right)=\rho a\left( \dfrac{5h}{2} \right) \\
 & \Rightarrow \dfrac{3}{2}=\dfrac{5a}{2} \\
 & \therefore a=\dfrac{3}{5}g \\
\end{align}$

Note:
The liquid that has a higher density as compared to the other will have lower height in the vertical tube, because the denser liquid will exert more pressure on the less dense liquid due to which the less dense liquid will attain a greater height in the vertical column.