Question

A vertical tower stands on a declivity which is inclined at ${15^ \circ }$ to the horizon. From the foot of the tower, a man ascends the declivity for $80$ feet and then finds that the tower subtends at an angle of ${30^ \circ }$. Find the height of the tower.

Answer 1

Hint: One side of the triangle is given that is $80$ feet and the subtended angle form by the tower is ${30^ \circ }$. Since the inclined angle is ${15^ \circ }$, the second angle of a triangle can be found by ${90^ \circ } - {15^ \circ }$, and the third angle is \[{180^ \circ } - (30 + 75)\] .
There are two angles and one side is known.
$\therefore $ apply the sine rule in the triangle. The Sine Rule can be applied in any triangle where one side and its opposite angle are known.
Here, use the Sine formula,
$ \Rightarrow$ $\dfrac{a}{{\operatorname{Sin} A}} = \dfrac{b}{{\operatorname{Sin} B}}$
$ \Rightarrow$ $\dfrac{{80}}{{\operatorname{Sin} {{75}^ \circ }}} = \dfrac{b}{{\operatorname{Sin} {{30}^ \circ }}}$
Here, $b$ is the height of the tower.

Complete answer:
Consider the vertical height of the tower is $AB$. The declivity is the downward slope inclined at ${15^ \circ }$ to the horizon.

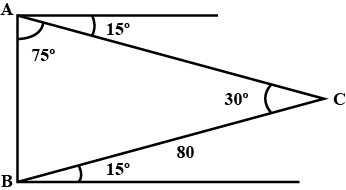
From the above figure the side $BC$ of the triangle $ABC$ is $80$ feet and the tower subtends an angle $C$ is ${30^ \circ }$ .
$\therefore \angle BCA = {30^ \circ }$
Here, vertical pole $AB$ is making ${90^ \circ }$ with the horizon.
Find the angle $\angle ABC$ ,
$ \Rightarrow$ $\angle ABC = {90^ \circ } - {15^ \circ }$
$ \Rightarrow$ $\angle ABC = {75^ \circ }$
The sum of the angles of the triangle is ${180^ \circ }$. In the triangle$ABC$,
$ \Rightarrow$ $\angle A + \angle B + \angle C = {180^ \circ }$
Substitute, $\angle B = {75^ \circ }$,$\angle C = {30^ \circ }$ into the formula and find $\angle A$,
$ \Rightarrow$ $\angle A + {75^ \circ } + {30^ \circ } = {180^ \circ }$
$ \Rightarrow$ $\angle A + {105^ \circ } = {180^ \circ }$
Simplify the equation by subtracting ${105^ \circ }$ from each side of the equation,
$ \Rightarrow$ $\angle A = {180^ \circ } - {105^ \circ }$
$ \Rightarrow$ $\angle A = {75^ \circ }$
Apply the Sine rule of the triangle,
If a, b and c are the sides of the triangle and their corresponding opposite angles are A , B and C then,
$ \Rightarrow$ $\dfrac{a}{{\operatorname{Sin} A}} = \dfrac{b}{{\operatorname{Sin} B}} = \dfrac{c}{{\operatorname{Sin} C}}$
Substitute, $a = {80^ \circ }$, $A = {75^ \circ }$ and $C = {30^ \circ }$ into the Sine Rule,
$ \Rightarrow$ $\dfrac{a}{{\operatorname{Sin} A}} = \dfrac{c}{{\operatorname{Sin} C}}$
$ \Rightarrow$ $\dfrac{{80}}{{\operatorname{Sin} {{75}^ \circ }}} = \dfrac{c}{{\operatorname{Sin} {{30}^ \circ }}}$
Here, $c = AB$ and, it is the height of the tower.
$ \Rightarrow$ $\dfrac{{80}}{{\operatorname{Sin} {{75}^ \circ }}} = \dfrac{c}{{\operatorname{Sin} {{30}^ \circ }}}$
$ \Rightarrow$ $c = \dfrac{{80 \times \operatorname{Sin} {{30}^ \circ }}}{{\operatorname{Sin} {{75}^ \circ }}}$
Write the angle ${75^ \circ }$ as the sum of ${45^ \circ }$ and ${30^ \circ }$.
$ \Rightarrow$ $c = \dfrac{{80 \times \sin {{30}^ \circ }}}{{\sin ({{45}^ \circ } + {{30}^ \circ })}} \ldots (1)$
First solve, $\sin ({45^ \circ } + {30^ \circ })$ by using the trigonometric addition formula of sine ;
$ \Rightarrow$ $\sin (A + B) = \sin A\cos B + \cos A\sin B$
Substitute $A = {45^ \circ }$ and $B = {30^ \circ }$ into the formula,
$ \Rightarrow$ $\sin ({45^ \circ } + {30^ \circ }) = \sin {45^ \circ }\cos {30^ \circ } + \cos {45^ \circ }\sin {30^ \circ }$
Use the trigonometric values, $\sin {45^ \circ } = \dfrac{1}{{\sqrt 2 }}$ , $\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}$, $\cos {45^ \circ } = \dfrac{1}{{\sqrt 2 }}$ and $\sin {30^ \circ } = \dfrac{1}{2}$.
$ \Rightarrow$ $\sin ({45^ \circ } + {30^ \circ }) = \dfrac{1}{{\sqrt 2 }} \times \dfrac{{\sqrt 3 }}{2} + \dfrac{1}{{\sqrt 2 }} \times \dfrac{1}{2}$
$ \Rightarrow$ $\sin ({45^ \circ } + {30^ \circ }) = \dfrac{{\sqrt 3 }}{{2\sqrt 2 }} + \dfrac{1}{{2\sqrt 2 }}$
$ \Rightarrow$ $\sin ({45^ \circ } + {30^ \circ }) = \dfrac{{\sqrt 3 + 1}}{{2\sqrt 2 }} \ldots (2)$
Substitute equation $(2)$ into the equation $(1)$ and use $\sin {30^ \circ } = \dfrac{1}{2}$ .
$ \Rightarrow$ $c = \dfrac{{80 \times \dfrac{1}{2}}}{{\dfrac{{\sqrt 3 + 1}}{{2\sqrt 2 }}}}$
Simplify further calculation,
$ \Rightarrow$ $c = \dfrac{{40 \times 2\sqrt 2 }}{{\sqrt 3 + 1}}$
Rationalize the term by multiplying the numerator and denominator of the right hand side by $\sqrt 3 - 1$.
$ \Rightarrow$ $c = \dfrac{{40 \times 2\sqrt 2 }}{{\sqrt 3 + 1}} \times \dfrac{{\sqrt 3 - 1}}{{\sqrt 3 - 1}}$
$ \Rightarrow$ $c = \dfrac{{40 \times 2\sqrt 2 (\sqrt 3 - 1)}}{{(\sqrt 3 + 1) \times (\sqrt 3 - 1)}}$
$ \Rightarrow$ $c = \dfrac{{40 \times 2\sqrt 2 (\sqrt 3 - 1)}}{{3 - 1}}$
$ \Rightarrow$ $c = \dfrac{{40 \times 2\sqrt 2 (\sqrt 3 - 1)}}{2}$
$ \Rightarrow$ $c = 40 \times \sqrt 2 (\sqrt 3 - 1)$
Multiply and simplify the calculation,
$ \Rightarrow$ $c = 40 \times (\sqrt 6 - \sqrt 2 )$

The height of the tower is $40 \times (\sqrt 6 - \sqrt 2 )$feet.

Note:
If It is asked to find the length of a side, you need to use the version of the Sine Rule where the lengths are on the top:
$ \Rightarrow$ $\dfrac{a}{{\operatorname{Sin} A}} = \dfrac{b}{{\operatorname{Sin} B}}$
You will only ever need two parts of the Sine Rule formula, not all three.
If It is asked to find the angle of the triangle, you need to use the version of the Sine Rule where the angles are on the top:
$ \Rightarrow$ $\dfrac{{\operatorname{Sin} A}}{a} = \dfrac{{\operatorname{Sin} B}}{b}$
Here, a is the side opposite to angle A and b is the side opposite to angle B.