Question

A vertical tower OP stands at the centre O of a square ABCD. Let h and b denote the length OP and AB respectively. Suppose \[\angle APB=60{}^\circ \] then the relationship between h and b can be expressed as
(a) $ 2{{b}^{2}}={{h}^{2}} $
(b) $ 2{{h}^{2}}={{b}^{2}} $
(c) $ 3{{b}^{2}}=2{{h}^{2}} $
(d) $ 2{{b}^{2}}=3{{h}^{2}} $

Answer 1

Hint: Start by drawing a rough diagram of the situation given in the figure. We know that the diagonals of the square are equal and bisect each other at the centre of the circle. We also know that the length of the diagonals of the square is $ \sqrt{2} $ times the length of the sides, so, we can say that $ OA=OB=\dfrac{\sqrt{2}b}{2}=\dfrac{b}{\sqrt{2}} $ . Now focus on the right angled triangles AOP and triangle BOP and apply Pythagoras theorem to find AP and BP. Now apply the cosine rule in triangle APB to reach the answer.

Complete step-by-step answer:
Let us start the solution to the above question by drawing a rough diagram of the situation given in the question.

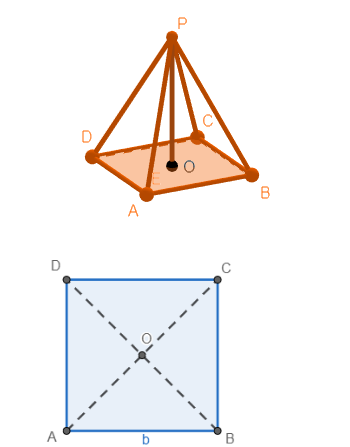
We know that the diagonals of the square are equal and bisect each other at the centre of the circle. We also know that the length of the diagonals of the square is $ \sqrt{2} $ times the length of the sides, so, we can say that $ OA=OB=\dfrac{\sqrt{2}b}{2}=\dfrac{b}{\sqrt{2}} $ .
Now if we focus on $ \Delta AOP $ , we will find that it is right angled at O, $ OA=\dfrac{b}{\sqrt{2}} $ and OP=h. So, if we apply Pythagoras theorem, we get
 $ {{\left( perpendicular \right)}^{2}}+{{\left( base \right)}^{2}}={{\left( hypotenuse \right)}^{2}} $
 $ \Rightarrow O{{P}^{2}}+A{{O}^{2}}=A{{P}^{2}} $
 $ \Rightarrow {{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}=A{{P}^{2}} $
 $ \Rightarrow \sqrt{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}}=AP.........(i) $
Similarly, if we focus on right angled triangle BOP, we will get
 $ \sqrt{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}}=BP.........(ii) $
Now we will focus on $ \Delta APB $ . Let us draw a separate diagram of it for better visualisation.

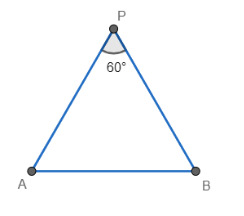
Now according to the cosine rule of triangle, $ \cos \left( \angle APB \right)=\dfrac{A{{P}^{2}}+B{{P}^{2}}-A{{B}^{2}}}{2\left( AP \right)\left( BP \right)} $ . If we substitute the values from equation (i) and (ii), we get
 $ \cos 60{}^\circ =\dfrac{{{\left( \sqrt{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}} \right)}^{2}}+{{\left( \sqrt{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}} \right)}^{2}}-{{b}^{2}}}{2\left( \sqrt{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}} \right)\left( \sqrt{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}} \right)} $
We know that $ \cos 60{}^\circ =\dfrac{1}{2} $ . If we put this in our equation, we get
 $ \dfrac{1}{2}=\dfrac{{{\left( \sqrt{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}} \right)}^{2}}+{{\left( \sqrt{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}} \right)}^{2}}-{{b}^{2}}}{2\left( \sqrt{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}} \right)\left( \sqrt{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}} \right)} $
 $ \Rightarrow \dfrac{1}{2}=\dfrac{{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}+{{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}}-{{b}^{2}}}{2\left( {{h}^{2}}+{{\left( \dfrac{b}{\sqrt{2}} \right)}^{2}} \right)} $
Now we will cancel the 2 in the denominators and cross multiply. On doing so, we get
 $ \dfrac{1}{2}=\dfrac{2{{h}^{2}}+{{b}^{2}}-{{b}^{2}}}{2\left( {{h}^{2}}+\dfrac{{{b}^{2}}}{2} \right)} $
 $ \Rightarrow {{h}^{2}}+\dfrac{{{b}^{2}}}{2}=2{{h}^{2}} $
 $ \Rightarrow \dfrac{{{b}^{2}}}{2}={{h}^{2}} $
 $ \Rightarrow {{b}^{2}}=2{{h}^{2}} $
Hence, the answer to the above question is option (b).

Note: The key thing is to draw the diagram correctly. Also, it is generally observed that students get afraid of the long equations, but here the equation might look big but all the terms are getting cancelled and giving us a simple result. Be careful about the calculations and sign as well, because it is generally seen that students make errors in the calculation part.