Question

A vertical stick 12 m long casts a shadow 8 m long on the ground. At the same time a tower casts the shadow 40 m long on the ground. Determine the height of the tower.
(a) 50m
(b) 60 m
(c) 40 m
(d) None of these

Answer 1

Hint: The angle of depression of the stick and the tower is the same because both these shadows are casting on the ground at the same time. Therefore the trigonometric ratio of tangent of angle of depression is the same which is equal to the perpendicular divided by the base. Let us assume that the height of the tower is “h”. Now, equate the ratio of height of the stick to the shadow with the ratio of height of the tower to the shadow of the tower.

Complete step-by-step answer:
In the below diagram, we have shown the vertical stick of 12 m and its shadow of 8 m with the angle of depression as $\theta $ and we have also shown that the tower is casting a shadow of 40 m.
 

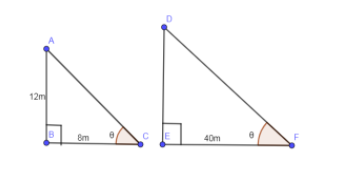
In the above diagram, AB is the vertical stick and DE is the tower. As the shadow is casting at the same time so the angle of depression is the same in both the cases which we have shown by $\theta $.
The angle of depression is the same in both the cases so the tangent of $\theta $ is also same in both the cases.
Now, we are going to find $\tan \theta $ for $\Delta ABC$.
We know that,
$\tan \theta =\dfrac{P}{B}$
In the above formula, “P” stands for the perpendicular of the triangle corresponding to angle $\theta $ and “B” stands for the base of the triangle corresponding to angle $\theta $.
Using this relation, we can find the value of $\tan \theta $ for $\Delta ABC$.

$\tan \theta =\dfrac{P}{B}$

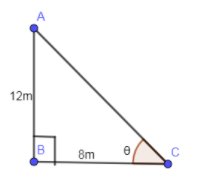
In the above triangle, “P” equal to 12 m and “B” equal to 8 m so substituting these values in the above equation we get,
$\begin{align}
  & \tan \theta =\dfrac{12}{8} \\
 & \Rightarrow \tan \theta =\dfrac{3}{2}.......Eq.(1) \\
\end{align}$
Now, we are going to find $\tan \theta $ for $\Delta DEF$.

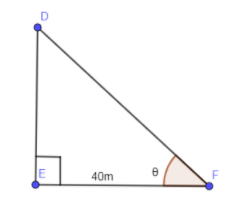
Let us assume that the height of the tower is “h” which is DE in the above diagram.
$\tan \theta =\dfrac{h}{40}$………. Eq. (2)
Equating eq. (1) and eq. (2) we get,
$\dfrac{3}{2}=\dfrac{h}{40}$
On cross multiplication of the above equation we get,
$\begin{align}
  & 120=2h \\
 & \Rightarrow h=60m \\
\end{align}$
From the above, we have calculated the height of the tower as 60 m.
Hence, the correct option is (b).

Note: The question demands the understanding of $\tan \theta $ and what it is equal to. It also demands that you should understand the meaning of “that both the tower and the vertical stick is casting the shadow at the same time”. If you don’t understand that the casting of the shadows at the same time means that the angle of depression is the same in both the tower and the vertical stick case then you cannot solve this problem.