Question

A vertical pole stands at a point O on a horizontal ground. A and B are points on the ground $ 10m $ apart. The pole subtends an angle $ {30^0} $ and $ {60^0} $ at A and B respectively. Then the height of the tower equals.
(A) $ 10\sqrt 3\;m $
(B) $ 5\sqrt 3\;m $
(C) $ 15\sqrt 3\;m $
(D) None of these

Answer 1

Hint: Use the triangle property of $ \tan \theta $ to calculate the unknown variables using the given conditions. To solve this question, we will assume that the pole stands vertically upward on the ground making angle $ {90^0} $ with the ground.

Complete step-by-step answer:
Observe that diagram

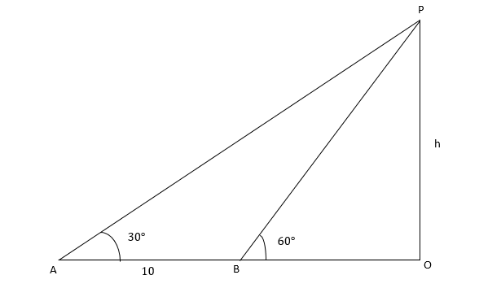
It is given in the question that,
 $ \angle PAO = {30^0} $
 $ \angle PBO = {60^0} $
 $ AB = 10 m $
We have to find the height of the tower.
Let us assume that the height of the tower be $ h $
Let us consider the $ \Delta PAO $
In $ \Delta PAO $
Using the triangle properties of trigonometric function, we can write
 $ \tan \angle PAO = \dfrac{h}{{OA}} $
 $ \Rightarrow \tan {30^0} = \dfrac{h}{{OA}} $
From the figure, we can observe that
 $ OA = AB + BO $
 $ \Rightarrow OA = 10 + BO $
Therefore, we get
 $ \tan {30^0} = \dfrac{h}{{10 + BO}} $
By substituting the value of $ \tan {30^0} = \dfrac{1}{{\sqrt 3 }} $ in above equation, we can write
 $ \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{10 + BO}} $
By cross multiplying the above equation, we get
 $ 10 + BO = h\sqrt 3 $
 $ \Rightarrow BO = h\sqrt 3 - 10 $
Now let us consider the triangle \[\Delta PBO\]
In \[\Delta PBO\]
Using the triangle properties of trigonometric function, we can write
 $ \tan \angle PBO = \dfrac{h}{{OB}} $
 $ \Rightarrow \tan {60^0} = \dfrac{h}{{OB}} $
By substituting the value of $ \tan {60^0} = \sqrt 3 $ and the value of $ OB = h\sqrt 3 - 10 $ calculated above, we can write
 $ \sqrt 3 = \dfrac{h}{{h\sqrt 3 - 10}} $
By cross multiplying, we get
 $ \sqrt 3 (h\sqrt 3 - 10) = h $
By simplifying it, we get
 $ 3h - 10\sqrt 3 = h $
 $ \Rightarrow 2h = 10\sqrt 3 $
Dividing both the sides by $ 2 $ we get
 $ h = 5\sqrt 3 $
So, the height of the tower is $ 5\sqrt 3\; m $
Therefore, form the above explanation, the correct answer is, option (B) $ 5\sqrt 3\;m $
So, the correct answer is “Option B”.

Note: To use the triangle properties of a trigonometric function, we need to have a right angled triangle. Therefore, we cannot question the above if we do not consider the pole to be perpendicular to the ground. We have given two conditions to solve. In such a case, we use one condition to find one variable and the substitute that variable into the second condition to get the final answer. Just like we did in the above question by finding the value of BO using the first condition and the substituting that value into the second condition to find the height of the tower.