Question

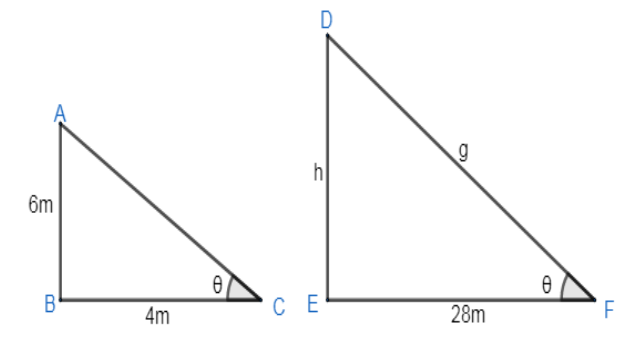
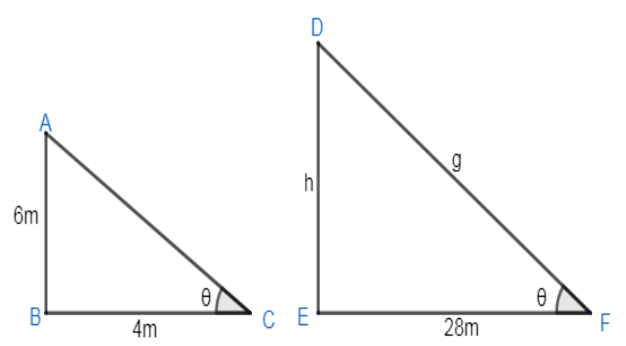
A vertical pole of length 6m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28m long. Find the height of the tower.

Answer 1

Hint:We will be using the concepts of height and distance to solve the problem. We will be using trigonometry to further simplify the solution. We will be using the fact that the angle of inclination of the sun is the same for all objects at a particular time. We will start by finding the ratio $\tan \theta =\dfrac{p}{B}$, where p is perpendicular and B is base, from triangle ABC and then from triangle DEF. Equating these two ratios, we will be able to find the height of the tower.

Complete step-by-step solution:
Now we have been given a vertical pole of 6m which casts a shadow of 4m on the ground and at the same time, a tower casts a shadow 28m long.

We have let the angle of inclination be $\theta$ in $\Delta \text{ABC}$. We know that $\tan \theta =\dfrac{p}{B}$ .
Where P is perpendicular and B is base. Therefore,
$\begin{align}
  & \tan \theta =\dfrac{AB}{BC} \\
 & =\dfrac{6}{4} \\
\end{align}$
$\tan \theta =\dfrac{3}{2}$ …………………… (1)
Now, we will apply $\tan \theta$ in $\Delta \text{DEF}$. We know that $\tan \theta =\dfrac{p}{B}$
$\begin{align}
  & \tan \theta =\dfrac{DE}{EF} \\
 &\Rightarrow \tan \theta =\dfrac{DE}{28} \\
\end{align}$
Now, we will substitute the value of $\tan \theta$ from (1)
$\dfrac{3}{2}=\dfrac{DE}{28}$
On cross multiply we have
$\begin{align}
  & 3\times 28=2\times DE \\
 &\Rightarrow DE=\dfrac{3\times 28}{2} \\
 &\Rightarrow DE=3\times 14 \\
 &\Rightarrow DE=42m \\
\end{align}$
Therefore, the height of tower DE=42.

Note: To solve these types of questions it is important to note the fact that the sun has the same angle of inclination for all objects at a particular time also one must know some important trigonometric formulae like $\tan \theta =\dfrac{Perpendicular}{Hypotenuse}$. Students can also try using the Pythagoras theorem and finding the perpendicular from triangle ABC and proceed or they might try to compute the angle. But, this is not required here, since the angle for both the cases would be the same. So, they can directly apply the tangent ratio, equate them, and get the answer.