Question

A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.

Answer 1

Hint: First of all, make the figures and name the vertices which will give us an idea of what we have to find. These types of questions usually form a triangular shape. Observe the figure carefully and see if these two figures have any kind of similarity. Then taking this similarity into consideration proceed for the rest of the calculations.

Complete step by step answer:
Given,
Height of pole = AB = 6 m
Length of shadow of pole = BC = 4 m
Length of shadow of tower = EF = 28 m

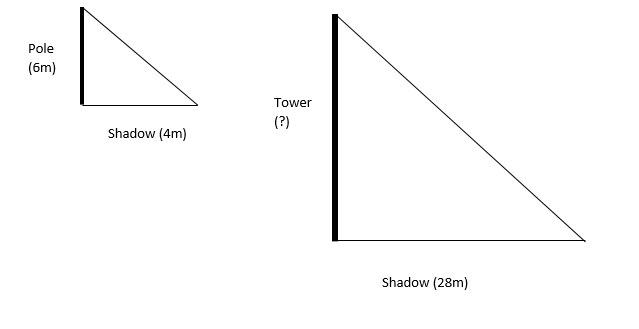
In \[\Delta ABC\] and \[\Delta DEF\]
\[
   \Rightarrow \angle B = \angle E = 90^\circ {\text{ }}\left[ {\because {\text{as both are vertical to ground}}} \right] \\
   \Rightarrow \angle C = \angle F{\text{ }}\left[ {\because {\text{same angle of elevation in both the cases as both shadows are casted at the same time}}} \right] \\
  \therefore \Delta ABC \cong \Delta DEF{\text{ by AA similarity criterion}} \\
\]
We know that if two triangles are similar, ratio of their sides are in proportion
So, \[\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}}\]
\[
   \Rightarrow \dfrac{6}{{DE}} = \dfrac{4}{{28}} \\
   \Rightarrow DE = 6 \times 7 = 42m \\
\]

Hence, the height of the tower is 42 m.

Note: Two triangles are said to be similar when they have two corresponding angles congruent and the sides proportional. The area, altitude, and the volume of similar triangles are in the same ratio as the ratio of the length of their sides. ‘\[ \cong \]’ is the symbol of similarity.